Article contents
On the Spectra of Unbounded Subnormal Operators
Published online by Cambridge University Press: 20 November 2018
Extract
Putnam showed in [5] that the spectrum of the real part of a bounded subnormal operator on a Hilbert space is precisely the projection of the spectrum of the operator onto the real line. (In fact he proved this more generally for bounded hyponormal operators.) We will show that this result can be extended to the class of unbounded subnormal operators with bounded real parts.
Before proceeding we establish some notation. If T is a (not necessarily bounded) operator on a Hilbert space, then D(T) will denote its domain, and σ(T) its spectrum. For K a subspace of D(T), T|K will denote the restriction of T to K. Norms of bounded operators and elements in Hilbert spaces will be indicated by ‖ ‖. All Hilbert space inner products will be written 〈,〉. If W is a set in C, the closure of W will be written clos W, the topological boundary will be written bdy W, and the projection of W onto the real line will be written π(W),
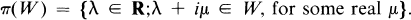
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1986
References
- 9
- Cited by


