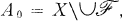Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Colbourn, Martenc Jones
1985.
Annals of Discrete Mathematics (26): Algorithms in Combinatorial Design Theory.
Vol. 114,
Issue. ,
p.
67.
Gionfriddo, Mario
1987.
Combinatorial Design Theory.
Vol. 149,
Issue. ,
p.
189.
Füredi, Zoltán
1988.
Matchings and covers in hypergraphs.
Graphs and Combinatorics,
Vol. 4,
Issue. 1,
p.
115.
Eugeni, Franco
and
Gionfriddo, Mario
1989.
On the minimum number of blocks of a maximal partial spread in STS(v) and SQS(v).
Journal of Geometry,
Vol. 36,
Issue. 1-2,
p.
37.
Pippenger, Nicholas
and
Spencer, Joel
1989.
Asymptotic behavior of the chromatic index for hypergraphs.
Journal of Combinatorial Theory, Series A,
Vol. 51,
Issue. 1,
p.
24.
Tuza, Zs.
1992.
Combinatorics '90 - Recent Trends and Applications, Proceedings of the Conference on Corn binatorics, Gaeta.
Vol. 52,
Issue. ,
p.
545.
Alon, Noga
Kim, Jeong-Han
and
Spencer, Joel
1997.
Nearly perfect matchings in regular simple hypergraphs.
Israel Journal of Mathematics,
Vol. 100,
Issue. 1,
p.
171.
Kim, Jeong Han
2001.
Nearly Optimal Partial Steiner Systems.
Electronic Notes in Discrete Mathematics,
Vol. 7,
Issue. ,
p.
74.
Goodall, Andrew
and
de Mier, Anna
2011.
Spanning trees of 3-uniform hypergraphs.
Advances in Applied Mathematics,
Vol. 47,
Issue. 4,
p.
840.
Erzurumluoğlu, Aras
and
Pike, David A.
2018.
Twofold triple systems with cyclic 2‐intersecting Gray codes.
Journal of Combinatorial Designs,
Vol. 26,
Issue. 4,
p.
154.
Stinson, Douglas R.
2021.
On partial parallel classes in partial Steiner triple systems.
Discrete Mathematics,
Vol. 344,
Issue. 4,
p.
112279.
Keevash, Peter
Pokrovskiy, Alexey
Sudakov, Benny
and
Yepremyan, Liana
2022.
New bounds for Ryser’s conjecture and related problems.
Transactions of the American Mathematical Society, Series B,
Vol. 9,
Issue. 8,
p.
288.
Kang, Dong Yeap
Kühn, Daniela
Methuku, Abhishek
and
Osthus, Deryk
2023.
New bounds on the size of nearly perfect matchings in almost regular hypergraphs.
Journal of the London Mathematical Society,
Vol. 108,
Issue. 5,
p.
1701.
Montgomery, Richard
2024.
Surveys in Combinatorics 2024.
p.
131.
Im, Seonghyuk
Kim, Jaehoon
Lee, Joonkyung
and
Methuku, Abhishek
2024.
A proof of the Elliott–Rödl conjecture on hypertrees in Steiner triple systems.
Forum of Mathematics, Sigma,
Vol. 12,
Issue. ,
 ) be a Steiner triple system on v = |X| points, and suppose that
) be a Steiner triple system on v = |X| points, and suppose that 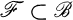 is a partial parallel class (transversal, clear set, set of pairwise disjoint blocks) of maximum size
is a partial parallel class (transversal, clear set, set of pairwise disjoint blocks) of maximum size 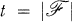 . We want to derive a bound on
. We want to derive a bound on 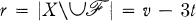 . (I conjecture that in fact r is bounded, e.g., r ≦ 4 – 4 is attained for the Fano plane, but all that has been proved so far (cf. [1], [2]) are bounds r < C.v for some C. Here we shall prove r < 5v2/3.)
. (I conjecture that in fact r is bounded, e.g., r ≦ 4 – 4 is attained for the Fano plane, but all that has been proved so far (cf. [1], [2]) are bounds r < C.v for some C. Here we shall prove r < 5v2/3.)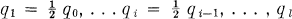 , where l is determined by ql ≧ 6,
, where l is determined by ql ≧ 6, 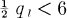 , i.e.,
, i.e.,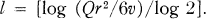
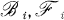 as follows. Let
as follows. Let