Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-27T18:56:08.057Z Has data issue: false hasContentIssue false
  • English
  • Français

On the roots of polynomials with log-convex coefficients

Part of: General convexity Geometric function theory

Published online by Cambridge University Press:  15 February 2022

María A. Hernández Cifre Open the ORCID record for María A. Hernández Cifre [Opens in a new window] ,
Miriam Tárraga  and
Jesús Yepes Nicolás Open the ORCID record for Jesús Yepes Nicolás [Opens in a new window]
María A. Hernández Cifre*
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo, 30100 Murcia, Spain e-mail: [email protected] [email protected]
Miriam Tárraga
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo, 30100 Murcia, Spain e-mail: [email protected] [email protected]
Jesús Yepes Nicolás
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo, 30100 Murcia, Spain e-mail: [email protected] [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the family of nth degree polynomials whose coefficients form a log-convex sequence (up to binomial weights), and investigate their roots. We study, among others, the structure of the set of roots of such polynomials, showing that it is a closed convex cone in the upper half-plane, which covers its interior when n tends to infinity, and giving its precise description for every 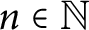$n\in \mathbb {N}$ , 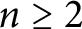$n\geq 2$ . Dual Steiner polynomials of star bodies are a particular case of them, and so we derive, as a consequence, further properties for their roots.

Keywords

Dual Steiner polynomialsdual quermassintegralslog-convex sequenceslog-convex coefficients polynomialsproperties of roots

MSC classification

Primary: 52A30: Variants of convex sets (star-shaped, ($m, n$)-convex, etc.) 52A39: Mixed volumes and related topics
Secondary: 30C15: Zeros of polynomials, rational functions, and other analytic functions (e.g. zeros of functions with bounded Dirichlet integral)
Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 2 , April 2023 , pp. 470 - 493
Check for updates
Copyright
© Canadian Mathematical Society, 2022

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research is part of the project PGC2018-097046-B-I00, supported by MCIN/AEI/10.13039/501100011033/FEDER “Una manera de hacer Europa.” It is also supported by Fundación Séneca, project 19901/GERM/15.

References

Alonso-Gutiérrez, D., Henk, M., and Hernández Cifre, M. A., A characterization of dual quermassintegrals and the roots of dual Steiner polynomials. Adv. Math. 331(2018), 565–588.CrossRefGoogle Scholar
Conway, J. B., Functions of one complex variable. 2nd ed., Springer-Verlag, New York, 1978.CrossRefGoogle Scholar
Davenport, H. and Pólya, G., On the product of two power series. Canad. J. Math. 1(1949), no. 1, 1–5.CrossRefGoogle Scholar
Green, M. and Osher, S., Steiner polynomials, Wulff flows, and some new isoperimetric inequalities for convex plane curves. Asian J. Math. 3(1999), no. 3, 659–676.CrossRefGoogle Scholar
Hardy, G., Littlewood, J. E., and Pólya, G., Inequalities. Reprint of the 1952 ed., Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1988.Google Scholar
Henk, M. and Hernández Cifre, M. A., Notes on the roots of Steiner polynomials. Rev. Mat. Iberoamericana 24(2008), no. 2, 631–644.CrossRefGoogle Scholar
Henk, M. and Hernández Cifre, M. A., On the location of roots of Steiner polynomials. Bull. Braz. Math. Soc. 42(2011), no. 1, 153–170.CrossRefGoogle Scholar
Henk, M., Hernández Cifre, M. A., and Saorín, E., Steiner polynomials via ultra-logconcave sequences. Commun. Contemp. Math. 14(2012), no. 6, 1–16.CrossRefGoogle Scholar
Hernández Cifre, M. A. and Saorín, E., Differentiability of quermassintegrals: A classification of convex bodies. Trans. Amer. Math. Soc. 366(2014), 591–609.Google Scholar
Hernández Cifre, M. A. and Tárraga, M., On the (dual) Blaschke diagram. Bull. Braz. Math. Soc. 52(2021), 291–305.CrossRefGoogle Scholar
Jetter, M., Bounds on the roots of the Steiner polynomial. Adv. Geom. 11(2011), 313–319.CrossRefGoogle Scholar
Katsnelson, V., On H. Weyl and J. Steiner Polynomials. Complex Anal. Oper. Theory 3(2009), no. 1, 147–220.CrossRefGoogle Scholar
Lutwak, E., Dual mixed volumes. Pacific J. Math. 58(1975), no. 2, 531–538.CrossRefGoogle Scholar
Lutwak, E., Dual cross-sectional measures. Atti Accad. Naz. Lincei 58(1975), 1–5.Google Scholar
Marden, M., Geometry of polynomials. 2nd ed., Mathematical Surveys, 3, American Mathematical Society, Providence, RI, 1966.Google Scholar
Milovanović, G. V., Mitrinović, D. S., and Rassias, T. M., Topics in polynomials: Extremal problems, inequalities, zeros, World Scientific, Singapore, 1994.CrossRefGoogle Scholar
Schneider, R., Convex bodies: The Brunn-Minkowski theory. 2nd expanded ed., Cambridge University Press, Cambridge, 2014.Google Scholar
Shephard, G. C., Inequalities between mixed volumes of convex sets. Mathematika 7(1960), 125–138.CrossRefGoogle Scholar