Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Weinstein, J.
1974.
Large Matchings in Graphs.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 6,
p.
1498.
Grünbaum, B.
1974.
Matchings in polytopal graphs.
Networks,
Vol. 4,
Issue. 2,
p.
175.
Bollobás, B.
and
Eldridge, S. E.
1976.
Maximal matchings in graphs with given minimal and maximal degrees.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 79,
Issue. 2,
p.
221.
Bollobás, Béla
1977.
Extremal problems in graph theory.
Journal of Graph Theory,
Vol. 1,
Issue. 2,
p.
117.
Bollobás, B.
Saito, Akira
and
Wormald, N. C.
1985.
Regular factors of regular graphs.
Journal of Graph Theory,
Vol. 9,
Issue. 1,
p.
97.
1986.
Matching Theory.
Vol. 121,
Issue. ,
p.
483.
Galanc, Tadeusz
and
Mikuś, Jan
1986.
The choice of an optimum group of experts.
Technological Forecasting and Social Change,
Vol. 30,
Issue. 3,
p.
245.
Zhou, Sanming
2000.
Inequalities involving independence domination, f-domination, connected and total f-domination numbers.
Czechoslovak Mathematical Journal,
Vol. 50,
Issue. 2,
p.
321.
Gao, Hang
and
Gao, Wenyu
2018.
Maximum matching and kernelization of edge dominating set.
Information Processing Letters,
Vol. 136,
Issue. ,
p.
21.


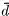 possesses a set of at least
possesses a set of at least 