Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:25:12.252Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Nonsquare Constants of Orlicz Spaces with Orlicz Norm

Published online by Cambridge University Press:  20 November 2018

Yaqiang Yan
Yaqiang Yan*
Affiliation:
Department of Mathematics, Suzhou University, Suzhou, Jiangsu 215006, People's Republic of China, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 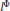${{l}^{\Phi }}$ and 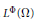${{L}^{\Phi }}\left( \Omega \right)$ be the Orlicz sequence space and function space generated by 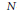$N$-function 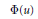$\Phi (u)$ with Orlicz norm. We give equivalent expressions for the nonsquare constants 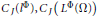${{C}_{J}}\left( {{l}^{\Phi }} \right),\,{{C}_{J}}\left( {{L}^{\Phi }}\left( \Omega \right) \right)$ in sense of James and 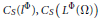${{C}_{S}}\left( {{l}^{\Phi }} \right),\,{{C}_{S}}\left( {{L}^{\Phi }}\left( \Omega \right) \right)$ in sense of Schäffer. We are devoted to get practical computational formulas giving estimates of these constants and to obtain their exact value in a class of spaces 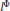${{l}^{\Phi }}$ and 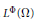${{L}^{\Phi}}\left(\Omega \right)$.

Keywords

46E30James nonsquare constantSchäffer nonsquare constantOrlicz sequence spaceOrlicz function space
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 1 , 01 February 2003 , pp. 204 - 224
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Chen, S. T., Non-squareness of Orlicz spaces. Chinese Ann.Math. Ser. A 6 (1985), 619–624.Google Scholar
[2] Chen, S. T., Geometry of Orlicz spaces. Dissertation Math. 356 (1996), 17–23.Google Scholar
[3] Cui, Y. A., Weakly convergent sequence coefficient in Köthe sequence spaces. Proc. Amer.Math. Soc. (1) 126 (1998), 195–210.Google Scholar
[4] Gao, J. and Lau, K. S., On the geometry of spheres in normed linear spaces. J. Austral.Math. Soc. Ser. A 48 (1990), 101–112.Google Scholar
[5] Hudzik, H., Uniformly non-l(1) n Orlicz spaces with Luxemburg norm. Studia Math. 81 (1985), 271–284.Google Scholar
[6] Ji, D. H. and Wang, T. F., Nonsquare constants of normed spaces. Acta. Sci. Math. (Szeged) 59 (1994), 719–723.Google Scholar
[7] Ji, D. H. and Zhan, D. P., Some equivalent representations of nonsquare constants and its applications. Northeast. Math. J. (4) 15 (1999), 439–444.Google Scholar
[8] Krasnoselskiĭ, M. A. and Rutickiĭ, Ya. B., Convex Functions and Orlicz Spaces. Noordhoff, Groningen, 1961.Google Scholar
[9] Rao, M. M. and Ren, Z. D., Packing in Orlicz sequence spaces. Studia Math. 126 (1997), 235–251.Google Scholar
[10] Ren, Z. D., Nonsquare constants of Orlicz spaces. Lecture Notes in Pure and Applied Math. 186 (1997), 179–197.Google Scholar
[11] Wang, T. F., Packing constants of Orlicz sequence spaces. Chinese Ann.Math. Ser. A 8 (1987), 508–513.Google Scholar
[12] Wang, Y. W. and Chen, S. T., Non squareness, B-convexity and flatness of Orlicz spaces. Comment. Math. Prace. Mat. 28 (1988), 155–165.Google Scholar
[13] Yan, Y. Q., Some results on packing in Orlicz sequence spaces. Studia Math. (1) 147 (2001), 73–88.Google Scholar
[14] Yan, Y. Q., Computation of Nonsquare Constants of Orlicz Spaces. J. Austral. Math. Soc., to appear.Google Scholar