Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T06:03:01.106Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Mackey Borel Structure

Published online by Cambridge University Press:  20 November 2018

L. Terrell Gardner
L. Terrell Gardner*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

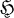Let A be a C*-algebra and a Hilbert space which is infinite dimensional and of Hilbert dimension ≧ dim π for all π ∈ Â. Suppose that the set Irr 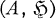of all non-null *-representations π of A on 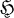, irreducible on the essential space 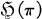, is given the relative strong topology as a subspace of Rep 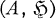[2; 4; 6]. That is, the topology is that of simple convergence in 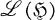with the strong topology. Finally, let ∼ denote equivalence of representations in Irr 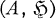implemented by partial isometries in 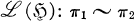if and only if there exists a partial isometry 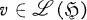with vv* ⊃ H(π1) and v*v ⊃ H(π2) satisfying π2(a) = v*π1(a)v for all a ∈ A.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 4 , August 1971 , pp. 674 - 678
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Auslander, L. and Moore, C. C., Unitary representations of solvable Lie groups, Amer. Math. Soc. Memoir No. 62 (Amer. Math. Soc, Providence, 1966).Google Scholar
2. Bichteler, K., A generalization to the non-separable case of Takesaki's duality theorem for C*-algebras, Invent. Math. 9 (1969), 89–98.Google Scholar
3. Dixmier, J., Dual et quasi-dual d'une algèbre de Banach involutive, Trans. Amer. Math. Soc. 104 (1962), 278–283.Google Scholar
4. Dixmier, J., les C*-algèbres et leurs representations (Gauthiers-Villars, Paris, 1969).Google Scholar
5. Effros, E., Transformation groups and C*-algebras, Ann. of Math. 81 (1965), 38–55.Google Scholar
6. Gardner, L. T., On the “third definition” of the topology on the spectrum of a C*-algebra, Can. J. Math. 28 (1971), 445–450.Google Scholar