Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:04:45.500Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Lusternik-Schnirelmann Category of Maps

Published online by Cambridge University Press:  20 November 2018

Donald Stanley
Donald Stanley*
Affiliation:
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

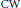We give conditions which determine if cat of a map go up when extending over a cofibre. We apply this to reprove a result of Roitberg giving an example of a $\text{CW}$ complex 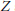$Z$ such that 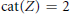$\text{cat}(Z)\,=\,2$ but every skeleton of 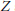$Z$ is of category 1. We also find conditions when 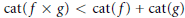$\text{cat}(f\,\times \,g)\,<\,\text{cat}(f)\,+\,\text{cat}(g)$. We apply our result to show that under suitable conditions for rational maps 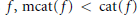$f,\,\text{mcat}(f)\,<\,\text{cat}(f)$ is equivalent to 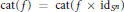$\text{cat(}f)\,=\,\text{cat(}f\,\times \,\text{i}{{\text{d}}_{{{S}^{n}}}})$. Many examples with 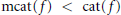$\text{mcat}(f)\,<\,\text{cat}(f)$ satisfying our conditions are constructed. We also answer a question of Iwase by constructing 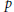$p$-local spaces 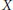$X$ such that 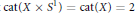$\text{cat(}X\ \times \,{{S}^{1}}\text{)}\,\text{=}\,\text{cat(}X\text{)}\,\text{=2}$. In fact for our spaces and every 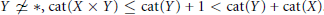$Y\,\not{\simeq }\,*,\,\text{cat}(X\,\times \,Y)\,\le \,\text{cat}(Y)\,+\,1\,\text{cat}(Y)\,+\,\text{cat}(X)$. We show that this same 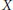$X$ has the property 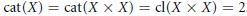$\text{cat}(X)=\,\text{cat}(X\,\times \,X)\,=\,\text{cl}(X\,\times \,X)\,=\,2$.

Keywords

55M3055P62
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 3 , 01 June 2002 , pp. 608 - 633
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Arkowitz, M., The generalized Whitehead product. Pacific J. Math. 12 (1962), 7–23.Google Scholar
[2] Arkowitz, M. and Stanley, D., The cone length of a product of co-H-spaces and a problem of Ganea. Bull. London Math. Soc., to appear.Google Scholar
[3] Baues, H. J., Iterierte Join-Konstructionen. Math. Zeit. 131 (1973), 77–84.Google Scholar
[4] Berstein, I. and Ganea, T., The category of a map and of a cohomology class. Fund. Math. 50 (1961), 265–279.Google Scholar
[5] Berstein, I. and Hilton, P. J., Category and Generalized Hopf Invariants. Illinois J. Math. 4 (1960), 437–451.Google Scholar
[6] Bousfield, A. K., Localization of spaces with respect to homology. Topology 14 (1975), 133–150.Google Scholar
[7] Bousfield, A. K. and Gugenheim, V. K. A. M., On PL De Rham theory and rational homotopy type. Mem. Amer. Math. Soc. 179, 1976.Google Scholar
[8] Cohen, D. E., Products and carrier theory. Proc. London Math. Soc. 7 (1957), 219–248.Google Scholar
[9] Felix, Y., La dichotomie elliptique-hyperbolique en homotopie rationnelle. Astérisque 176, 1989.Google Scholar
[10] Felix, Y. and Halperin, S., Rational L.S. category and its applications. Trans. Amer. Math. Soc. 273 (1982), 1–37.Google Scholar
[11] Felix, Y., Halperin, S. and Lemaire, J.-M., The rational LS category of products and Poincaré duality complexes. Topology 37 (1998), 749–756.Google Scholar
[12] Fernandez, L., Thesis. Université de Lille 1, 1998.Google Scholar
[13] Fox, R. H., On the Lusternik-Schnirelmann Category. Ann.Math. 42 (1941), 333–370.Google Scholar
[14] Ganea, T., A generalization of the homology and homotopy suspension. Comm. Math. Helv. 39 (1965), 295–322.Google Scholar
[15] Ganea, T., Lusternik-Schnirelmann Category and Strong Category. Illinois J. Math. 11 (1967), 417–427.Google Scholar
[16] Gray, B., Spaces of the same n-type, for all n. Topology 5 (1966), 241–243.Google Scholar
[17] Halperin, S., Lectures on minimal models. Mém. Soc. Math France (N.S.), 9–10, 1983.Google Scholar
[18] Halperin, S. and Lemaire, J.-M., Notions of Category in Differential Algebra. Springer Lecture Notes in Mathematics 1318 (1988), 138–154.Google Scholar
[19] Idrissi, E., Un exemple o`u M cat(f) ≠ A cat(f). C. R. Acad. Sci. Paris 310 (1990), 599–602.Google Scholar
[20] Iwase, N., Ganea's conjecture on Lusternik-Schnirelmann category. Bull. London Math. Soc. 30 (1998), 623–634.Google Scholar
[21] Iwase, N., A1-method in Lusternik-Schnirelmann category. Topology, to appear.Google Scholar
[22] James, I. M., On category in the sense of Lusternik-Schnirelmann. Topology 17 (1978), 331–348.Google Scholar
[23] James, I. M., Lusternik-Schnirelmann category. In: Handbook of algebraic topology, North-Holland, Amsterdam, 1995, 1293–1310.Google Scholar
[24] Lusternik, L. and Schnirelmann, L., Méthodes topologiques dans les problèmes variationnels. Inst. for Math. and Mechanics, Moscow, 1930. (In Russian)Google Scholar
[25] Lusternik, L. and Schnirelmann, L., Méthodes topologiques dans les problèmes variationnels. Hermann, Paris, 1934.Google Scholar
[26] Mather, M., Pull-backs in Homotopy Theory. Canad. J. Math. 28 (1976), 225–263.Google Scholar
[27] Milnor, J., On spaces having the homotopy type of a CW complex. Trans. Amer. Math. Soc. 90 (1959), 272–280.Google Scholar
[28] Parent, P.-E., LS Category: Product Formulas. Topology Appl. 106 (2000), 35–47.Google Scholar
[29] Porter, G. J., The Homotopy Groups ofWedges of Suspensions. Amer. J. Math. 88 (1966), 655–663.Google Scholar
[30] Quillen, D., Homotopical algebra. Lecture Notes in Math. 43, Springer-Verlag, Berlin-New York, 1967.Google Scholar
[31] Roitberg, J., The Lusternik-Schnirelmann category of certain infinite CW complexes. Topology 39 (2000), 95–101.Google Scholar
[32] Scheerer, H. and Stanley, D., On the rational LS category of a cartesian product of maps. Preprint, 1998.Google Scholar
[33] Scheerer, H. and Stelzer, M., Fibrewise infinite symmetric products and M-category. Bull. Korean Math. Soc. 36 (1999), 671–682.Google Scholar
[34] Scheerer, H. and Tanré, D., Fibrations à la Ganea. Bull. Belg. Math. Soc. 4 (1997), 333–353.Google Scholar
[35] Stanley, D., Spaces with Lusternik-Schnirelmann category n and cone length n + 1. Topology 39 (2000), 985–1019.Google Scholar
[36] Steenrod, N., A convenient category of topological spaces. Michigan Math. J. 14 (1967), 133–152.Google Scholar
[37] Sullivan, D., Infinitesimal computations in topology. Inst. Hautes E´tudes Sci. Publ. Math. 47 (1977), 269–331.Google Scholar
[38] Switzer, R. M., Algebraic Topology—Homotopy and Homology. Springer-Verlag, 1975.Google Scholar
[39] Takens, F., The Lusternik-Schnirelman Categories of a Product Space. Compositio Math. 22 (1970), 175–180.Google Scholar
[40] Tanré, D., Homotopie Rationnelle: Modèles de Chen, Quillen, Sullivan. Lecture Notes in Math. 1025, Springer-Verlag, Berlin, 1983.Google Scholar
[41] Toda, H., Composition Methods in Homotopy Groups of Spheres. Princeton University Press, 1962.Google Scholar
[42] Vogt, R. M., Convenient categories of topological spaces for homotopy theory. Arch.Math. 22 (1971), 545–555.Google Scholar
[43] Whitehead, G. W., Elements of Homotopy Theory. Springer-Verlag, 1978.Google Scholar
[44] Zabrodsky, A., On phantom maps and a theorem of H. Miller. Israel J. Math. 58 (1987), 129–143.Google Scholar