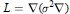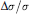Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berestycki, H.
Hamel, F.
and
Monneau, R.
2000.
One-dimensional symmetry of bounded entire solutions of some elliptic equations.
Duke Mathematical Journal,
Vol. 103,
Issue. 3,
Ambrosio, Luigi
and
Cabré, Xavier
2000.
Entire solutions of semilinear elliptic equations in ℝ³ and a conjecture of De Giorgi.
Journal of the American Mathematical Society,
Vol. 13,
Issue. 4,
p.
725.
Barlow, Martin T.
Bass, Richard F.
and
Gui, Changfeng
2000.
The Liouville property and a conjecture of De Giorgi.
Communications on Pure and Applied Mathematics,
Vol. 53,
Issue. 8,
p.
1007.
Jerison, David
and
Monneau, Régis
2004.
Towards a counter-example to a conjecture of De Giorgi in high dimensions.
Annali di Matematica Pura ed Applicata,
Vol. 183,
Issue. 4,
p.
439.
Priola, Enrico
and
Zabczyk, Jerzy
2004.
Liouville theorems for non-local operators.
Journal of Functional Analysis,
Vol. 216,
Issue. 2,
p.
455.
Froese, Richard
2005.
Liouville's Theorem in the Radially Symmetric Case.
Canadian Mathematical Bulletin,
Vol. 48,
Issue. 3,
p.
405.
Moschini, Luisa
2005.
New Liouville theorems for linear second order degenerate elliptic equations in divergence form.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 22,
Issue. 1,
p.
11.
Pinchover, Yehuda
2007.
A Liouville-type Theorem for Schrödinger Operators.
Communications in Mathematical Physics,
Vol. 272,
Issue. 1,
p.
75.
Fazly, Mostafa
and
Sire, Yannick
2019.
Symmetry properties for solutions of nonlocal equations involving nonlinear operators.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 36,
Issue. 2,
p.
523.
Fazly, Mostafa
and
Gui, Changfeng
2020.
On nonlocal systems with jump processes of finite range and with decays.
Journal of Differential Equations,
Vol. 268,
Issue. 6,
p.
3171.
Villegas, Salvador
2021.
Sharp Liouville Theorems.
Advanced Nonlinear Studies,
Vol. 21,
Issue. 1,
p.
95.
Takeda, Masayoshi
2022.
Criticality of Schrödinger forms and Liouville‐type property.
Mathematische Nachrichten,
Vol. 295,
Issue. 2,
p.
395.
Fazly, Mostafa
2023.
De Giorgi type results for equations with nonlocal lower-order terms.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 202,
Issue. 2,
p.
519.