Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T01:11:28.249Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Hankel and Some Related Transformations

Published online by Cambridge University Press:  20 November 2018

P. Heywood  and
P. G. Rooney
P. Heywood
Affiliation:
University of Edinburgh, Edinburgh, Scotland
P. G. Rooney
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The transformations we will discuss in this paper are the Hankel transformation Hυ defined for f ∊ C0, the collection of continuous functions compactly supported in (0, ∞), by

(1.1)

and the and transformations defined for such f by

(1.2)

and

(1.3)

where Jv >and Yv are the Bessel functions of the first and second kinds respectively, and Hv is the Struve function; for the theory of these functions see [1, Chapter VII].

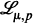These transformations were studied extensively by one of us in [5] and [6] on the spaces defined in [7; Sections 1 & 5]. In those papers the boundedness of the three transformations was fully given on the spaces 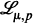for 1 < p < ∞, but not for p = 1. Also inversion formulae were given for the transformations only for portions of their respective ranges of boundedness.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 4 , 01 August 1988 , pp. 989 - 1009
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Erdelyi, A. et al., Higher transcendental functions I & II (New York, McGraw-Hill, 1953).Google Scholar
2. Erdelyi, A. et al., Tables of integral transforms I & II (New York, McGraw-Hill, 1954).Google Scholar
3. Heywood, P. and Rooney, P. G., On the inversion of the even and odd Hilbert transformations, Proc. Roy. Soc. Edinburgh 109A, 201–211.Google Scholar
4. Rooney, P. G., On the ranges of certain fractional integrals, Can J. Math. 24 (1972), 1198–1216.Google Scholar
5. Rooney, P. G., A technique for studying the boundedness and extendability of certain types of operators, Can. J. Math. 25 (1973), 1090–1102.Google Scholar
6. Rooney, P. G., On and transformations, Can. J. Math. 32 (1980), 1021–1044.Google Scholar
7. Rooney, P. G., On the integral transformations with G-function kernels, Proc. Roy. Soc. Edinburgh 93A (1983), 265–297.Google Scholar
8. Stein, E. M., Interpolation of linear operators, Trans. Amer. Math. Soc. 87 (1958), 159–172.Google Scholar
9. Titchmarsh, E. C., The theory of Fourier integrals (Oxford U.P., 1937).Google Scholar