Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T02:02:53.395Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Galois Theory of Commutative Rings II: Automorphisms induced in Residue Rings

Published online by Cambridge University Press:  20 November 2018

Carl Faith
Carl Faith*
Affiliation:
Rutgers University, New Brunswick, New Jersey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a group of automorphisms of a commutative ring K, and let KG denote the Galois subring consisting of all elements left fixed by every g in G. An ideal M is G-stable, or G-invariant, provided that g(x) lies in M for every x in M, that is, g(M) ⊆ M, for every g in G. Then, every g in G induces an automorphism 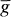in the residue ring 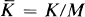, and if 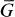is the group consisting of all 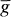, trivially

1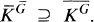

When the inclusion (1) is strict, then G is said to be cleft at M, or by M, and otherwise G is uncleft at (by) M. When G is cleft at all ideals except 0, then G is cleft, and uncleft otherwise.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 5 , 01 October 1987 , pp. 1025 - 1037
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Auslander, M. and Goldman, O., The Brauer group of a commutative ring, Trans. Amer. Math. Soc. 97 (1960), 367–409.Google Scholar
2. Chase, S. U., Harrison, D. K. and Rosenberg, A., Galois theory and Galois cohomology of commutative rings, Memoirs A.M.S. 52 (1965), 15–33.Google Scholar
3. DeMeyer, F. and Ingraham, E., Separable algebras over commutative rings, Lecture Notes in Math. 181 (Springer-Verlag, Berlin, Heidelberg and New York, 1971).CrossRefGoogle Scholar
4. Faith, C., Galois extensions of commutative rings, Math. J. Okayama U. 18 (1976), 113–116.Google Scholar
5. Faith, C., On the Galois theory of commutative rings I: Dedekind's theorem on the independence of automorphisms revisited, in Algebraist's Hommage, Proceedings of the Yale Symposium in honor of Nathan Jacobson, New Haven (1981), Contemporary Math. 73(1982), 183–192.Google Scholar
6. Faith, C., Algebra II: Ring theory, (Springer-Verlag, 1976).CrossRefGoogle Scholar
7. Kaplansky, I., A theorem on division rings, Can. J. Math. 3 (1951), 290–292.Google Scholar
8. Shamsuddin, A., Rings with automorphisms leaving no nontrivial proper ideals invariant, Proceedings of the Conference on Algebra and Geometry, Kuwait University, Khaldiya, Kuwait.CrossRefGoogle Scholar
9. Vasconcelos, W., On local and stable cancellation, An. Acad. Brasil, Ci 37 (1965), 389–393.Google Scholar
10. Vasconcelos, W., On finitely generated flat modules, Trans. A.M.S. 138 (1969), 505–512.Google Scholar
11. Vasconcelos, W., Injective endomorphisms of finitely generated modules, Proc. A.M.S. 25 (1970), 900–901.Google Scholar