Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:03:36.110Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Distribution of the Sequence n2θ (mod 1)

Published online by Cambridge University Press:  20 November 2018

J. B. Friedlander  and
H. Iwaniec
J. B. Friedlander
Affiliation:
University of Toronto, Toronto, Ontario
H. Iwaniec
Affiliation:
Institute for Advanced Study, Princeton, New Jersey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a paper with the above title H. Heilbronn [4] proved that, given any real θ, there exist infinitely many positive integers n such that the distance ║θn2║ from θn2 to its nearest integral neighbour satisfies the bound

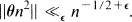
He actually proved a somewhat stronger statement which shows that the integers n occur with some regularity and he suggested that perhaps the exponent 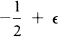may be replaced by . This theorem has attracted considerable attention and spawned a number of generalizations (see [1], [7] and the references therein), yet no essential improvement has been given for the original problem (but see [6], [8]).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 2 , 01 April 1987 , pp. 338 - 344
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Baker, R. C., Recent results on fractional parts of polynomials, Number Theory, Carbondale (1979), 10–18, Lecture Notes in Math. 751 (Springer, Berlin, 1979).Google Scholar
2. Bombieri, E. and Iwaniec, H., On the order of ζ(½ + it), Ann. Sc. Abrm. Sup. Pisa (to appear).Google Scholar
3. Friedlander, J. B. and Iwaniec, H., Incomplete Kloosterman sums and a divisor problem, Annals of Math. 121 (1985), 319–350.Google Scholar
4. Heilbronn, H., On the distribution of the sequence n2θ (mod 1), Quart. J. Math. (Oxford) 19 (1948), 249–256.Google Scholar
5. Hooley, C., On the greatest prime factor of a cubic polynomial, J. Reine Angew. Math. 303/304 (1918), 21–50.Google Scholar
6. Hooley, C., On a new technique and its applications to the theory of numbers, Proc. London Math. Soc. (3) 38 ( 1979), 115–151.Google Scholar
7. Schmidt, W. M., Small fractional parts of polynomials, Regional Conference Series in Math. 32 (A.M.S., Providence, 1977).Google Scholar
8. Tenenbaum, G., Sur la concentration moyenne des diviseurs, Comm. Math. Helv. 60 (1985), 411–428.Google Scholar