Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T15:34:59.301Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Dispersive Estimate for the Dirichlet Schrödinger Propagator and Applications to Energy Critical NLS

Published online by Cambridge University Press:  20 November 2018

Dong Li ,
Guixiang Xu  and
Xiaoyi Zhang
Dong Li
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2. e-mail: [email protected]
Guixiang Xu
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, China, 100088. e-mail: xu [email protected]
Xiaoyi Zhang
Affiliation:
Department of Mathematics, University of Iowa, Iowa City, IA, USA, 52242 and Chinese Academy of Science, Beijing, China. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the obstacle problem for the Schrödinger evolution in the exterior of the unit ball with Dirichlet boundary condition. Under radial symmetry we compute explicitly the fundamental solution for the linear Dirichlet Schrödinger propagator 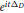${{e}^{it{{\Delta }_{D}}}}$ and give a robust algorithm to prove sharp 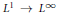${{L}^{1}}\,\to \,{{L}^{\infty }}$ dispersive estimates. We showcase the analysis in dimensions 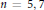$n\,=\,5,\,7$. As an application, we obtain global well-posedness and scattering for defocusing energy-critical 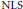$\text{NLS}$ on 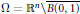$\Omega \,=\,{{\mathbb{R}}^{n}}\backslash \overline{B\left( 0,\,1 \right)}$ with Dirichlet boundary condition and radial data in these dimensions.

Keywords

35P2535Q5547J35Dirichlet Schrödinger propagatordispersive estimateDirichlet boundary conditionscattering theoryenergy critical
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 5 , 01 October 2014 , pp. 1110 - 1142
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Anton, R., Global existence for defocusing cubic NLS and Gross-Pitaveskii equations in three dimensional exterior domains. J. Math. Pures Appl. 89(2008), no. 4, 335–354. http://dx.doi.org/10.1016/j.matpur.2007.12.006 Google Scholar
[2] Burq, N., Gérad, P., and Tzvetkov, N., On nonlinear Schrödinger equations in exterior domains. Ann. Inst. H. Poincaré Anal. Non Linéaire 21(2004), no. 3, 295–318. http://dx.doi.org/10.1016/j.anihpc.2003.03.002 Google Scholar
[3] Burq, N., Lebeau, G., and Planchon, F., Global existence for energy critical waves in 3-D domains. J. Amer. Math. Soc. 21(2008), no. 3, 831–845 http://dx.doi.org/10.1090/S0894-0347-08-00596-1.Google Scholar
[4] Blair, M. D., Smith, H. F., and Sogge, C. D., Strichartz estimates for the wave equation on manifolds with boundary. Ann. Inst. H. Poincaré Anal. Non Linéaire 26(2009), no. 5, 1817–1829. http://dx.doi.org/10.1016/j.anihpc.2008.12.004 Google Scholar
[5] Blair, M. D., Strichartz estimates and the nonlinear SchrÖdinger equation on manifolds with boundary. Math. Ann. 354(2012), no. 4, 1397–1430. http://dx.doi.org/10.1007/s00208-011-0772-y Google Scholar
[6] Bourgain, J., Global well-posedness of defocusing critical nonlinear Schrödinger equation in the radial case. J. Amer. Math. Soc. 12(1999), no. 1, 145–171.Google Scholar
[7] Cazenave, T. and Weissler, F. B., The Cauchy problem for the critical nonlinear Schrödinger equation in Hs. Nonlinear Anal. 14(1990), no. 10, 807–836. http://dx.doi.org/10.1016/0362-546X(90)90023-A Google Scholar
[8] Colliander, J., Keel, M., Staffilani, G., Takaoka, H., and Tao, T. , Global well-posedness and scattering for the energy-critical nonlinear Schrödinger equation in R3. Ann. of Math. 167(2008), no. 3, 767–865.Google Scholar
[9] Dodson, B., Global well-posedness and scattering for the defocusing, energy-critical, nonlinear Schrödinger equation in the exterior of a convex obstacle when d = 4. ar Anal. 14(1990), no. 10, 807–836. arxiv:1112.0710 Google Scholar
[10] Grillakis, M., On nonlinear Schrödinger equations. Comm. Part. Differential Equations 25(2000), no. 9–10, 1827–1844. http://dx.doi.org/10.1080/03605300008821569 Google Scholar
[11] Ivanovici, O., Precise smoothing effect in the exterior of balls. Asymptot. Anal. 53(2007), no. 4, 189–208.Google Scholar
[12] Ivanovici, O., On the Schrödinger equation outside strictly convex obstacles. Anal. PDE 3(2010), no. 3, 261–293. http://dx.doi.org/10.2140/apde.2010.3.261 Google Scholar
[13] Keel, M. and Tao, T., Endpoint Strichartz estimates. Amer. J. Math. 120(1998), no. 5, 955–980. http://dx.doi.org/10.1353/ajm.1998.0039 Google Scholar
[14] Killip, R., M. Visan, and X. Zhang, Harmonic analysis outside a convex obstacle. arxiv:1205.5784 Google Scholar
[15] Killip, R., Quintic NLS in the exterior of a strictly convex obstacle. arxiv:1208.4904 Google Scholar
[16] Smith, D. Li, H., and Zhang, X., Global well-posedness and scattering for defocusing energy-critical NLS in the exterior of balls with radial data. Math. Res. Lett. 19(2012), no. 1, 213–232. http://dx.doi.org/10.4310/MRL.2012.v19.n1.a17 Google Scholar
[17] Ryckman, E. and Visan, M., Global well-posedness and scattering for the defocusing energy-critical nonlinear Schrödinger equation in R1+4. Amer. J. Math. 129(2007), no. 1, 1–60. http://dx.doi.org/10.1353/ajm.2007.0004 Google Scholar
[18] Smith, H. F. and Sogge, C. D., On the critical semilinear wave equation outside convex obstacles. J. Amer.Math. Soc. 8(1995), no. 4, 879–916. http://dx.doi.org/10.1090/S0894-0347-1995-1308407-1 Google Scholar
[19] Tao, T., Global well-posedness and scattering for the higher-dimensional energy-critical nonlinear Schrödinger equation for radial data. New York J. Math. 11(2005), 57–80.Google Scholar
[20] Visan, M., The defocusing energy-critical nonlinear Schrödinger equation in higher dimensions. Duke Math. J. 138(2007), no. 2, 281–374. http://dx.doi.org/10.1215/S0012-7094-07-13825-0 Google Scholar