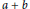Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
FAN, AI-HUA
2019.
Weighted Birkhoff ergodic theorem with oscillating weights.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 5,
p.
1275.
Mauduit, Christian
Rivat, Joël
and
Sárközy, András
2019.
On the distribution of the sum of digits of sums $$a+b$$ a + b.
The Ramanujan Journal,
Vol. 49,
Issue. 1,
p.
55.
Fan, Aihua
and
Konieczny, Jakub
2019.
On uniformity of q‐multiplicative sequences.
Bulletin of the London Mathematical Society,
Vol. 51,
Issue. 3,
p.
466.
Shparlinski, Igor E.
and
Thuswaldner, Jörg M.
2024.
Weyl Sums over Integers with Digital Restrictions.
Michigan Mathematical Journal,
Vol. 74,
Issue. 1,