Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:34:24.331Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Difference Property of the Class of Pointwise Discontinuous Functions and of Some Related Classes

Published online by Cambridge University Press:  20 November 2018

M. Laczkovich
M. Laczkovich*
Affiliation:
Eötvös Loránd University, Budapest, Hungary
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R denote the set of real numbers. For f:R → R and h ∈ R, the difference function Δhf is defined by

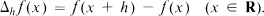
The function H:R → R is called additive if it satisfies Cauchy's equation

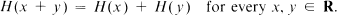
Let ℱ be a class of real valued functions defined on R. ℱ is said to have the difference property if, for every function f:R → R satisfying Δhf ∈ ℱ for every h ∈ R, there exists an additive function H such that f — H ∈ ℱ

It was conjectured by P. Erdos that the class of continuous functions has the difference property. This conjecture was proved by N. G. de Bruijn in [1], where the difference property of several other classes was verified as well. (For other references, see [6].)

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 36 , Issue 4 , 01 August 1984 , pp. 756 - 768
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. de Bruijn, N. G., Functions whose differences belong to a given class, Nieuw Archief voor Wiskunde 23 (1951), 194–218.Google Scholar
2. Erdös, P., Some remarks on set theory. Annals of Math. 44 (1943), 643–646.Google Scholar
3. Erdös, P., A theorem on the Riemann integral, Indaaationes Mathematicae 14 (1952), 142–144.Google Scholar
4. Hyers, D. H., On the stability of the linear functional equation, Proc. Nat. Acad. Sci. U.S.A. 27 (1941), 222–224.Google Scholar
5. Kuratowski, K., Topology (Academic Press, New York and London; PWN. Warsaw, 1966).Google Scholar
6. Laczkovich, M., Functions with measurable differences. Acta Math. Acad. Sci. Hungar. 35 (1980), 217–235.Google Scholar