Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-16T15:15:14.404Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Definition of C*-Algebras II

Published online by Cambridge University Press:  20 November 2018

Zoltán Magyar  and
Zoltán Sebestyén
Zoltán Magyar
Affiliation:
Eötvös Lorand University, Budapest, Hungary
Zoltán Sebestyén
Affiliation:
Eötvös Lorand University, Budapest, Hungary
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theory of noncommutative involutive Banach algebras (briefly Banach *-algebras) owes its origin to Gelfand and Naimark, who proved in 1943 the fundamental representation theorem that a Banach *-algebra with C*-condition

(C*)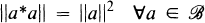

is *-isomorphic and isometric to a norm-closed self-adjoint subalgebra of all bounded operators on a suitable Hilbert space.

At the same time they conjectured that the C*-condition can be replaced by the B*-condition.

(B*)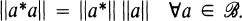

In other words any B*-algebra is actually a C*-algebra. This was shown by Glimm and Kadison [5] in 1960.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 4 , 01 August 1985 , pp. 664 - 681
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Aarnes, J. F. and Kadison, R. V., Pure states and approximate identities, Proc. Amer. Math. Soc. 21 (1969), 749–752.Google Scholar
2. Araki, H. and Elliott, G. A., On the definition of C*-algebras, Publ. Res. Inst, for Math. Sci. Kyoto Univ. 9 (1973), 93–112.Google Scholar
3. Bonsall, F. F. and Duncan, J., Complete normed algebras, Erg. Math. Bd. 80 (Springer, 1973).CrossRefGoogle Scholar
4. Doran, R. S. and Wichmann, J., The Gelfand-Naimark theorems for C*-algebras, L'Enseignement Mathém. 23 (1977), 153–180.Google Scholar
5. Glimm, J. G. and Kadison, R. V., Unitary operators in C*-algebras, Pac. J. Math. 10 (1960), 547–556.Google Scholar
6. Palmer, T. W., Characterizations of C*-algebras, Bull. Amer. Math. Soc. 74 (1968), 538–540.Google Scholar
7. Pták, V., Banach algebras with involution, Manuscripta Math. 6 (1972), 245–290.Google Scholar
8. Sakai, S., C*-algebras and W*-algebras, Erg. Math. Bd. 60 (Springer, 1971).Google Scholar
9. Sebestyén, Z., A weakening of the definition of C*-algebras, Acta Sci. Math. (Szeged) 35 (1973), 17–20.Google Scholar
10. Sebestyén, Z., On the definition of C*-algebras, Publ. Math., Debrecen 21 (1974), 207–217.Google Scholar
11. Sebestyén, Z., Axiomatikus vizsgálatok a C*-algebrák köréből (Investigations in axiomatic C*-algebra theory), Dissertation (1974) (In Hungarian).Google Scholar
12. Sebestyén, Z., Every C*-seminorm is automatically submultiplicative, Periodica Math. Hung. 10 (1979), 1–8.Google Scholar