Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:02:28.775Z Has data issue: false hasContentIssue false
  • English
  • Français

On The Convolution of a Box Spline With a Compactly Supported Distribution: Linear Independence for the Integer Translates

Published online by Cambridge University Press:  20 November 2018

Charles K. Chui  and
Amos Ron
Charles K. Chui
Affiliation:
Department of Mathematics Texas A & M University College Station, Texas 77843 U.S.A.
Amos Ron
Affiliation:
Amos Ron Center for the Mathematical Sciences and Computer Sciences Department University of Wisconsin-Madison 1210 West Dayton St. Madison, Wisconsin 53706 USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem of linear independence of the integer translates of μ * B, where μ is a compactly supported distribution and B is an exponential box spline, is considered in this paper. The main result relates the linear independence issue with the distribution of the zeros of the Fourier-Laplace transform, 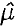of μ on certain linear manifolds associated with B. The proof of our result makes an essential use of the necessary and sufficient condition derived in [12]. Several applications to specific situations are discussed. Particularly, it is shown that if the support of μ is small enough then linear independence is guaranteed provided that 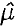does not vanish at a certain finite set of critical points associated with B. Also, the results here provide a new proof of the linear independence condition for the translates of B itself.

Keywords

box splinesexponential box splinescompactly supported functionsinteger translateslinear independencemultivariate splines41A6341A15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 1 , 01 February 1991 , pp. 19 - 33
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. de Boor, C., The polynomials in the linear span of integer translates of a compactly supported function, Constructive Approx. 3(1987), 199–208.Google Scholar
2. de Boor, C. and DeVore, R., Approximation by smooth multivariate splines, Trans. Amer. Math. Soc. 276(1983), 775–788.Google Scholar
3. de Boor, C. and Höllig, K., B-splines from parallelepipeds, J. d'Anal. Math. 42(1982/3), 99–115.Google Scholar
4. de Boor, C. and Höllig, K., Minimal support for bivariate splines, Approx. Theory and Its Appl. 3(1987), 11–23.Google Scholar
5. Ben-Artzi, A. and Ron, A., Translates of exponential box splines and their related spaces, Trans. Amer. Math. Soc. 309(1988), 683–710.Google Scholar
6. Chui, C.K. and He, T.X., On minimal and quasi-minimal supported bivariate splines, J. Approx. Theory 52(1988), 217–238.Google Scholar
7. Dahmen, W. and Micchelli, C.A., Multivariate E-splines, Advances in Math. 76(1989), 33–93.Google Scholar
8. Dyn, N. and Ron, A., Local Approximation by certain spaces of multivariate exponential polynomials, approximation order of exponential box splines and related interpolation problems, Trans. Amer. Math. Soc. 319(1990), 381–404.Google Scholar
9. Jia, R.Q. and Sivakumar, N., On the linear independence of integer translates of box splines with rational directions, Linear Alg. Appl., 135(1990),19–31.Google Scholar
10. Ron, A., Exponential box splines, Constructive Approx. 4(1988), 357–378.Google Scholar
11. Ron, A., Linear independence of the integer translates of an exponential box spline, Rocky Mount. J. Math., to appear.Google Scholar
12. Ron, A., A necessary and sufficient condition for the linear independence of the integer translates of a compactly supported distribution, Constructive Approx. 5(1989), 297–308.Google Scholar