Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T11:03:39.609Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Canonical Module of A 0-Dimensional Scheme

Published online by Cambridge University Press:  20 November 2018

Martin Kreuzer
Martin Kreuzer*
Affiliation:
Fakultätfür Mathematik Universität Regensburg Postfach 397 D-93040 Regensburg Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main topic of this paper is to give characterizations of geometric properties of O-dimensional subschemes 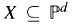in terms of the algebraic structure of the canonical module of their projective coordinate ring. We characterize Cayley- Bacharach, (higher order) uniform position, linearly and higher order general position properties, and derive inequalities for the Hilbert functions of such schemes. Finally we relate the structure of the canonical module to properties of the minimal free resolution of X.

Keywords

14C9913C05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 2 , 01 April 1994 , pp. 357 - 379
Copyright
Copyright © Canadian Mathematical Society 1994

References

[E] Eisenbud, D., Linear sections of ‘determinants varieties, Amer. J. Math. 110(1988), 541–575.Google Scholar
[EG] Eisenbud, D. and S. Goto, Linear free resolutions and minimal multiplicity, J. Algebra 88(1984), 89–133.Google Scholar
[EH] Eisenbud, D. and Harris, J., Finite projective schemes in linearly general position, J. Algebraic Geom. 1(1992), 15–30.Google Scholar
[EK] Eisenbud, D. and Koh, J.-H., Remarks on points in a projective space. In: Commutative Algebra, Math. Sci. Res. Inst. Publ. 15, Springer, New York, 1989.Google Scholar
[G] Gordon, W. J., A linear algebra proof of Clifford's theorem, Enseign. Math. 30(1984), 85–94. Google Scholar
[GKR] Geramita, A. V., Kreuzerand, M. Robbiano, L., Cayley-Bacharach schemes and their canonical modules, Trans. Amer. Math. Soc. 339(1993), 163–189.Google Scholar
[GW] Goto, S. and Watanabe, K., On graded rings I, J. Math. Soc. Japan 30(1978), 179–213.Google Scholar
[H] Harris, J., The genus of space curves, Math. Ann. 249(1980), 191–204.Google Scholar
[HE] Harris, J., (with the collaboration of D. Eisenbud), Curves in projective space, Sém. Math. Sup., Université de Montreal, 1982.Google Scholar
[Kl] Kreuzer, M., On 0-dimensional complete intersections, Math. Ann. 292(1992), 43–58.Google Scholar
[K2] Kreuzer, M., VektorbundelundderSatz von Cayley-Bacharach,RegQnsburgQrMath. Schriften 21, Universitât Regensburg, 1989.Google Scholar
[KK] Kreuzer, M. and Kunz, E., Traces in strict Frobenius algebras and strict complete intersections, J. Reine Angew. Math. 381(1987), 181–204.Google Scholar
[L] Lorenzini, A., Betti numbers of perfect homogeneous ideals, J. Pure Appl. Algebra 60(1989), 273–288.Google Scholar
[R] Rathmann, J., The uniform position principle for curves in characteristic p, Math. Ann. 276(1987), 565- 576.Google Scholar
[S] Schenzel, P., UberdiefreienAuflôsungenextremalerCohen-MacaulayRinge, J. Algebra 64(1980), 93–101.Google Scholar