Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:52:48.658Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Calkin Algebra and the Covering Homotopy Property, II

Published online by Cambridge University Press:  20 November 2018

John B. Conway
John B. Conway*
Affiliation:
Indiana University, Bloomington, Indiana
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a separable Hilbert space is the algebra of bounded linear operators on is the ideal of compact operators, and Π is the natural map of 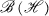onto the Calkin algebra .

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 1 , 01 February 1977 , pp. 210 - 215
Copyright
Copyright © Canadian Mathematical Society 1977

Footnotes

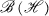This research was supported by a National Science Foundation (U.S.A.) Grant MPS 75-05266 A01.

References

1. Bratteli, O., Inductive limits of finite dimensional C*'-algebras, Trans. Amer. Math. Soc. 171 (1972), 195–234.Google Scholar
2. Brown, L. G., Douglas, R. G., and Fillmore, P. A., Unitary equivalence modulo the compact operators and extensions of C* algebras, Proc. Conf. on Operator Theory, Lecture Notes in Math., vol. 345 (Springer-Verlag, New York, 1973), 58–128.Google Scholar
3. Choi, M. D. and Effros, E. G., The completely positive lifting problem for C*-algebras, preprint.Google Scholar
4. Conway, J. B., On the Calkin algebra and the covering homotopy property, Trans. Amer. Math. Soc. 211 (1975), 135–142.Google Scholar
5. Michael, E., Continuous selections I, Ann. of Math. 63 (1956), 361–382.Google Scholar
6. Stratila, S. and Voiculescu, D., Representations of AF-Algebras and of the group £/(co)f Lecture Notes in Math. vol. 486, (Springer-Verlag, Berlin, 1975).Google Scholar
7. Voiculescu, D., A non-commutative Weyl-von Neumann theorem, preprint.Google Scholar