Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T00:59:17.274Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Asymptotic Growth ofBloch–Kato–Shafarevich–Tate Groups ofModular Forms Over CyclotomicExtensions

Published online by Cambridge University Press:  20 November 2018

Antonio Lei ,
David Loeffler  and
Sarah Livia Zerbes
Antonio Lei
Affiliation:
Département de mathématiques et de statistique, Pavillon Alexandre-Vachon, Université Laval, Qéubec, QC, Canada G1V 0A6 e-mail: [email protected]
David Loeffler
Affiliation:
Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL, UK e-mail: [email protected]
Sarah Livia Zerbes
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the asymptotic behaviour of the Bloch–Kato–Shafarevich–Tate group of a modular form 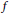$f$ over the cyclotomic 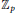${{\mathbb{Z}}_{p}}$-extension of 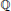$\mathbb{Q}$ under the assumption that 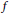$f$ is non-ordinary at $p$. In particular, we give upper bounds of these groups in terms of Iwasawa invariants of Selmer groups defined using $p$-adic Hodge Theory. These bounds have the same form as the formulae of Kobayashi, Kurihara, and Sprung for supersingular elliptic curves.

Keywords

11R1811F1111R2311F85cyclotomic extensionShafarevich-Tate groupBloch-Kato Selmer groupmodular formnon-ordinary primep-adic Hodge theory
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 4 , 01 August 2017 , pp. 826 - 850
Copyright
Copyright © Canadian Mathematical Society 2017

References

[Ber03] Berger, L., Block andKato's exponential map: three explicit formulas. Doc. Math. Extra Vol. 3(2003), 99–129.Google Scholar
[Ber04] Berger, L., Limites de représentations cristallines. Compos. Math. 140(2004), no. 6,1473–1498.http://dx.doi.Org/10.1112/S0010437X04000879 Google Scholar
[BK90] Bloch, S. and Kato, K., L-functions and Tamagawa numbers of motives. In: The Grothendieck Festschrift, Vol. I, Progr. Math., 86, Birkhäuser, Boston, MA, 1990, pp. 333–400.Google Scholar
[CC99] Cherbonnier, F. and Colmez, P., Théorie d'Iwasawa des représentations p-adiques d'un corps local. J. Amer. Math. Soc. 12(1999), no. 1, 241–268.http://dx.doi.org/10.1090/S0894-0347-99-00281-7 Google Scholar
[FL82] Fontaine, J.-M. and Laffaille, G., Construction de représentations p-adiques. Ann. Sci. École Norm. Sup. (4) 15(1982), no. 4, 547–608.Google Scholar
[Gil79] Gillard, R., Unités cyclotomiques, unités semi-locales et . Ann. Inst. Fourier (Grenoble) 29 (1979), no. 1, xiv, 49–79.Google Scholar
[KatO4] Kato, K., P-adic Hodge theory and values of zeta functions of modular forms. Astérisque 295(2004), ix, 117–290.Google Scholar
[Kob03] Kobayashi, S., Iwasawa theory for elliptic curves at super singular primes. Invent. Math. 152(2003), no. 1, 1–36.http://dx.doi.org/10.1007/s00222-002-0265-4 Google Scholar
[KurO2] Kurihara, M., On the Tate-Shafarevich groups over cyclotomic fields of an elliptic curve with supersingular reduction.I. Invent. Math. 149(2002), no. 1,195–224.http://dx.doi.org/10.1007/s002220100206 Google Scholar
[Leill] Lei, A., Iwasawa theory for modular forms at supersingular primes. Compos. Math. 147(2011), no. 3, 803–838.http://dx.doi.Org/10.1112/S0010437X10005130 Google Scholar
[Leil5] Lei, A., Bounds on the Tamagawa numbers of a crystalline representation over towers of cyclotomic extensions. Tohoku Math. J., to appear. Google Scholar
[LLZ10] Lei, A., Loeffler, D., and Zerbes, S. L., Wach modules and Iwasawa theory for modular forms. Asian J. Math. 14(2010), no. 4, 475–528.http://dx.doi.org/10.4310/AJM.2010.v14.n4.a2 Google Scholar
[LLZ11] Lei, A., Coleman maps and the p-adic regulator. Algebra Number Theory 5(2011), no. 8, 1095–1131.http://dx.doi.org/10.2140/ant.2011.5.1095 Google Scholar
[LZ13] Loeffler, D. and Zerbes, S. L., Wach modules and critical slope p-adic L-functions. J. Reine Angew. Math. 679(2013), 181–206.http://dx.doi.org/10.1515/crelle.2012.012 Google Scholar
[LZ14] Loeffler, D., Iwasawa theory and p-adic L-functions over extensions. Int. J. Number Theory 10(2014), no. 8, 2045–2096.http://dx.doi.Org/1 0.1142/S1793042114500699 Google Scholar
[Maz72] Mazur, B., Rational points ofabelian varieties with values in towers of number fields. Invent. Math. 18(1972), no. 3-4, 183–266.http://dx.doi.org/10.1007/BF01389815 Google Scholar
[PR94] Perrin-Riou, B., Théorie d'Iwasawa des représentations p-adiques sur un corps local. Invent. Math. 115(1994), no. 1, 81–161,http://dx.doi.org/10.1007/BF01231755 Google Scholar
[PR03] Perrin-Riou, B. , Arithmétique des courbes elliptiques à réduction supersinguliére en p. Experiment. Math. 12(2003), no. 2, 155–186.http://dx.doi.org/10.1080/10586458.2003.10504490 Google Scholar
[Spr12] Sprung, F. E. I., Iwasawa theory for elliptic curves at supersingular primes: a pair of main conjectures. J. Number Theor 132(2012), no. 7,1483–1506.http://dx.doi.0rg/IO.IOI6/j.jnt.2O11.11.003 Google Scholar
[Spr13] Sprung, F. E. I. , The Šafarevic-Tate group in cyclotomic -extensions at supersingular primes. J. Reine Angew. Math. 681(2013), 199–218.http://dx.doi.org/10.1515/crelle-2012-0031 Google Scholar
[Spr15] Sprung, F. E. I. , On pairs of p-adic L-functions for weight two modular forms. arxiv:1601.00010 Google Scholar