Let 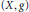$\left( X,\,g \right)$ be a complete noncompact Kähler manifold, of dimension 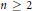$n\,\ge \,2$, with positive Ricci curvature and of standard type (see the definition below). N. Mok proved that $X$ can be compactified, i.e., $X$ is biholomorphic to a quasi-projective variety. The aim of this paper is to prove that the 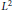${{L}^{2}}$ holomorphic sections of the line bundle 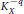$K_{X}^{-q}$ and the volume form of the metric $g$ have no essential singularities near the divisor at infinity. As a consequence we obtain a comparison between the volume forms of the Kähler metric $g$ and of the Fubini-Study metric induced on $X$. 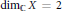In the case of ${{\dim}_{\mathbb{C}}}\,X\,=\,2$, we establish a relation between the number of components of the divisor 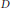$D$ and the dimension of the 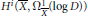${{H}^{i}}(\bar{X},\,\Omega \frac{1}{X}(\log \,D))$.