Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Carroll, Robert
1981.
Some Remarks on singular pseudodifferential operators.
Communications in Partial Differential Equations,
Vol. 6,
Issue. 12,
p.
1407.
1982.
Transmutation, Scattering Theory and Special Functions.
Vol. 69,
Issue. ,
p.
417.
Rooney, P. G.
1983.
On integral transformations with G-function kernels.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 93,
Issue. 3-4,
p.
265.
1985.
Transmutation Theory and Applications.
Vol. 117,
Issue. ,
p.
323.
Carroll, Robert
1986.
Patterns and structure in systems governed by linear second-order differential equations.
Acta Applicandae Mathematicae,
Vol. 6,
Issue. 2,
p.
109.
Rooney, P. G.
1986.
On the spectrum of an integral operator.
Glasgow Mathematical Journal,
Vol. 28,
Issue. 1,
p.
5.
Heywood, P.
and
Rooney, P.G.
1988.
On the inversion of the even and odd Hilbert transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 109,
Issue. 3-4,
p.
201.
Heywood, P.
and
Rooney, P.G.
1991.
On the inversion of the extended Hankel transformation.
Journal of Mathematical Analysis and Applications,
Vol. 160,
Issue. 1,
p.
284.
Heywood, P.
and
Rooney, P. G.
1994.
On the Struve Transformation.
SIAM Journal on Mathematical Analysis,
Vol. 25,
Issue. 2,
p.
450.
Heywood, P.
and
Rooney, P. G.
1995.
Lipschitz conditions satisfied by Hankel transforms.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 125,
Issue. 4,
p.
847.
Rooney, P. G.
1995.
On the representation of functions by the Hankel and some related transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 125,
Issue. 3,
p.
449.
Tuan, Vum Kim
1996.
On the range of the Y-transform.
Bulletin of the Australian Mathematical Society,
Vol. 54,
Issue. 2,
p.
329.
Borden, B.
1999.
Reduction of radar image artifacts caused by target inlets.
IEEE Transactions on Antennas and Propagation,
Vol. 47,
Issue. 5,
p.
898.
A.Kilbas, Anatoly
and
Trujillo, Juan J.
2000.
Generalized hankel transform no space.
Integral Transforms and Special Functions,
Vol. 9,
Issue. 4,
p.
271.
Kilbas, A.A.
and
Borovco, A.N.
2000.
Hardy-Titchmarsh And Hankel Type Transforms In -Spaces.
Integral Transforms and Special Functions,
Vol. 10,
Issue. 3-4,
p.
239.
Tuan, Vu Kim
2000.
On the Range of the Struve $\h_{\nu}-Transform.
Journal of Integral Equations and Applications,
Vol. 12,
Issue. 2,
Kilbas, Anatoly A.
and
Trujillo, Juan J.
2003.
Hankel-Schwartz and Hankel-Clifford transforms on % MathType!MTEF!2!1!+-% feaaeaart1ev0aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXanrfitLxBI9gBaerbd9wDYLwzYbItLDharqqt% ubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq% -Jc9vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0x% fr-xfr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyuam% aaBaaaleaacaaIXaGaaGimaaqabaGccqGH9aqpciGGSbGaaiOBaiaa% ysW7caWGRbWaaSbaaSqaaiaadsfacaaIXaaabeaakiaac+cacaWGRb% WaaSbaaSqaaiaadsfacaaIYaaabeaakiabg2da9iabgkHiTmaabmaa% baGaamyramaaBaaaleaacaWGHbaabeaakiaac+cacaWGsbaacaGLOa% GaayzkaaGaey41aq7aaiWaaeaadaqadaqaaiaadsfadaWgaaWcbaGa% aGOmaaqabaGccqGHsislcaWGubWaaSbaaSqaaiaaigdaaeqaaaGcca% GLOaGaayzkaaGaai4laiaacIcacaWGubWaaSbaaSqaaiaaikdaaeqa% aOGaaGjbVlaadsfadaWgaaWcbaGaamysaaqabaGccaGGPaaacaGL7b% GaayzFaaaaaa!5C4A! ${\cal L}_{\nu,p}$ -spaces.
Results in Mathematics,
Vol. 43,
Issue. 3-4,
p.
284.
Glaeske, Hans–Jürgen
and
Kilbas, Anatoly A.
2003.
A generalized Hankel transform on Lν,r–spaces.
Mathematische Nachrichten,
Vol. 258,
Issue. 1,
p.
16.
Gromak, Elena V.
and
Kilbas, Anatoly A.
2005.
Asymptotic expansions of 𝒴ηtransform.
Integral Transforms and Special Functions,
Vol. 16,
Issue. 5-6,
p.
407.
Kamoun, Lotfi
2007.
Besov-type spaces for the Dunkl operator on the real line.
Journal of Computational and Applied Mathematics,
Vol. 199,
Issue. 1,
p.
56.
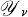 and
and 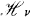 Transformations
Transformations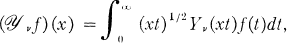
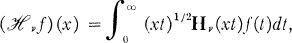
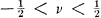 , each of the transformations is the inverse of the other.
, each of the transformations is the inverse of the other.