Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:13:15.152Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Addition of Relations in an Abelian Category

Published online by Cambridge University Press:  20 November 2018

P. J. Hilton  and
Y.-C. Wu
P. J. Hilton
Affiliation:
Cornell University, Ithaca, New York
Y.-C. Wu
Affiliation:
Case Western Reserve University, Cleveland, Ohio Oakland University, Rochester, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1] the category 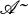of relations in an abelian category 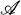was studied. A relation from A to B appeared as an equivalence class of pairs of 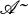-morphisms (ϕ, ψ),

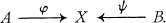
Moreover, this equivalence class may be written as the composite 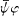, where 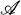is canonically embedded in 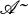and 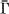is the image of Γ in the canonical involution on 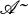. Every equivalence class has an essentially unique minimal representative (ϕ0,ψ0), characterized by the property that

where

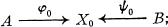
and 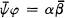if and only if the square

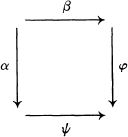
is exact.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 1 , 01 February 1970 , pp. 66 - 74
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Hilton, P. J., Correspondences and exact squares, Proc. Conf. Categorical Algebra (La Jolla, California, 1965), pp. 254–271 (Springer, New York, 1966).Google Scholar
2. Puppe, D., Korrespondenzen in Abelsche Kategorien, Math. Ann. 148 (1962), 1–30.Google Scholar