Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-16T17:30:32.331Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Absolute Cesaro Summability of Negative Order of a Series Associated with the Conjugate Series of a Fourier Series

Published online by Cambridge University Press:  20 November 2018

R. Mohanty  and
B. K. Ray
R. Mohanty
Affiliation:
Ravenshaw College, Cuttack (Orissa), India
B. K. Ray
Affiliation:
Ravenshaw College, Cuttack (Orissa), India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Definition. Let λ ≡ λ(ω) be continuous, differentiable, and monotonie increasing in (0, ∞) and let it tend to infinity as ω → ∞. A series 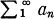an is summable |R, λ, r|, where r > 0, if

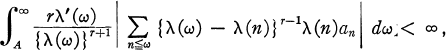
where A is a fixed positive number (6, Definition B).

Let f(t) be a periodic function with period 2π and Lebesgue integrable over (–π, π) and let

1.1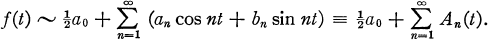

The series conjugate to (1.1), at t = x, is

1.2

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 552 - 557
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Bosanquet, L. S. and Hyslop, J. M., On the absolute summability of the allied series of a Fourier Series, Math. Z. 42 (1937), 489–512.Google Scholar
2. Chandrasekharan, K., The second theorem of consistency for absolutely summable series, J. Indian Math. Soc. (N.S.) 6 (1942), 168–180.Google Scholar
3. Hardy, G. H., Notes on some points in the integral calculus. LXVII: The arithmetic mean of a Fourier constant, Messenger of Math. 58 (1928), 50–52.Google Scholar
4. Hyslop, J. M., The absolute summability of series by Rieszian means, Proc. Edinburgh Math. Soc. (2) 5 (1936), 46–54.Google Scholar
5. Mazhar, S. M., A Tauberian theorem for absolute summability, Indian J. Math. 1 (1959), 69–76.Google Scholar
6. Mohanty, R., On the absolute Riesz summability of Fourier series and allied series, Proc. London Math. Soc. (2) 52 (1951), 295–320.Google Scholar
7. Mohanty, R. and Misra, B., On absolute logarithmic summability of a sequence related to a Fourier series, Tôhoku Math. J. (2) 6 (1954), 5–12.Google Scholar
8. Mohanty, R. and Mahapatra, S., On the absolute logarithmic summability of a Fourier series and its differentiated series, Proc. Amer. Math. Soc. 7 (1956), 254–259.Google Scholar
9. Mohanty, R. and Ray, B. K., On the behaviour of a series associated with the conjugate series of a Fourier series, Can. J. Math. 21 (1969), 535–551.Google Scholar
10. Varshney, O. P., On the absolute harmonic summability of a series related to a Fourier series, Proc. Amer. Math. Soc. 10 (1959), 784–789.Google Scholar