Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T16:58:31.346Z Has data issue: false hasContentIssue false
  • English
  • Français

On Surfaces in Three Dimensional Contact Manifolds

Published online by Cambridge University Press:  20 November 2018

Paul W. Y. Lee
Paul W. Y. Lee*
Affiliation:
The Chinese University of Hong Kong, Shatin, Hong Kong, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we introduce two quantities defined on a surface in a contact manifold. The first one is called degree of transversality 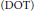$(\text{DOT})$, which measures the transversality between the tangent spaces of a surface and the contact planes. The second quantity, called curvature of transversality 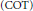$(\text{COT})$, is designed to give a comparison principle for 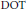$\text{DOT}$ along characteristic curves under bounds on 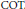$\text{COT}$. In particular, this gives estimates on lengths of characteristic curves, assuming 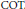$\text{COT}$ is bounded below by a positive constant.

We show that surfaces with constant 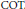$\text{COT}$ exist, and we classify all graphs in the Heisenberg group with vanishing 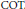$\text{COT}$. This is accomplished by showing that the equation for graphs with zero 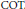$\text{COT}$ can be decomposed into two first order PDEs, one of which is the backward invisicid Burgers’ equation. Finally we show that the p-minimal graph equation in the Heisenberg group also has such a decomposition. Moreover, we can use this decomposition to write down an explicit formula of a solution near a regular point.

Keywords

35R03contact manifoldssubriemannian manifoldssurfaces
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 3 , 01 June 2013 , pp. 621 - 633
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Agrachev, A. and Lee, P.W. Y., Generalized Ricci curvature bounds for three dimensional contact subriemannian manifolds. arxiv:0903.2550. Google Scholar
[2] Agrachev, A., Bishop and Laplacian comparison theorems on three dimensional contact subriemannian manifolds with symmetry. arxiv:1105.2206. Google Scholar
[3] Arcozzi, N. and Ferrari, F., Metric normal and distance function in the Heisenberg group. Math. Z. 256(2007), no. 3, 661–684. http://dx.doi.org/10.1007/s00209-006-0098-8 Google Scholar
[4] Arcozzi, N., The Hessian of the distance from a surface in the Heisenberg group. Ann. Acad. Sci. Fenn. Math. 33(2008), no. 1, 35–63.Google Scholar
[5] Cheng, J.-H., Hwang, J.-F., Malchiodi, A., and Yang, P., Minimal surfaces in pseudohermitian geometry. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 4(2005), no. 1, 129–177.Google Scholar
[6] Cheng, J.-H., A Codazzi-like equation and the singular set for C1 smooth surfaces in the Heisenberg group. arxiv:1006.4455. Google Scholar
[7] Danielli, D., Garofalo, N., Nhieu, D. M., and Pauls, S. D., Instability of graphical strips and a positive answer to the Bernstein problem in the Heisenberg group H1. J. Differential Geom. 81(2009), no. 2, 251–295.Google Scholar
[8] Evans, L. C., Partial differential equations. Second ed., Graduate Studies in Mathematics, 19, American Mathematical Society, Providence, RI, 2010.Google Scholar
[9] Garofalo, N. and Pauls, S., The Bernstein problem in the Heisenberg group. arxiv:math/0209065. Google Scholar
[10] Hurtado, A., Ritoré, M., and Rosales, C., The classification of complete stable area-stationary surfaces in the Heisenberg group H1. Adv. Math. 224(2010), no. 2, 561–600. http://dx.doi.org/10.1016/j.aim.2009.12.002 Google Scholar
[11] Pauls, S. D., H-minimal graphs of low regularity in H1. Comment. Math. Helv. 81(2006), no. 2, 337–381. http://dx.doi.org/10.4171/CMH/55 Google Scholar
[12] Pauls, S. D., Minimal surfaces in the Heisenberg group. Geom. Dedicata 104(2004), 201–231. http://dx.doi.org/10.1023/B:GEOM.0000022861.52942.98 Google Scholar
[13] M. Ritoré, and C. Rosales, , Area-stationary surfaces in the Heisenberg group H1. Adv. Math. 219(2008), no. 2, 633–671. http://dx.doi.org/10.1016/j.aim.2008.05.011 Google Scholar