Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T21:11:50.689Z Has data issue: false hasContentIssue false
  • English
  • Français

On Special Fiber Rings of Modules

Part of: Chain conditions, finiteness conditions Commutative algebra: Homological methods General commutative ring theory Local rings and semilocal rings Theory of modules and ideals

Published online by Cambridge University Press:  09 January 2019

Cleto B. Miranda-Neto
Cleto B. Miranda-Neto*
Affiliation:
Departamento de Matemática, Universidade Federal da Paraíba, 58051-900 João Pessoa, Paraíba, Brazil Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove results concerning the multiplicity as well as the Cohen–Macaulay and Gorenstein properties of the special fiber ring 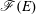$\mathscr{F}(E)$ of a finitely generated 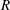$R$-module 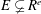$E\subsetneq R^{e}$ over a Noetherian local ring 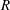$R$ with infinite residue field. Assuming that 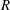$R$ is Cohen–Macaulay of dimension 1 and that 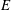$E$ has finite colength in 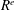$R^{e}$, our main result establishes an asymptotic length formula for the multiplicity of 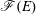$\mathscr{F}(E)$, which, in addition to being of independent interest, allows us to derive a Cohen–Macaulayness criterion and to detect a curious relation to the Buchsbaum–Rim multiplicity of 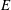$E$ in this setting. Further, we provide a Gorensteinness characterization for 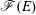$\mathscr{F}(E)$ in the more general situation where 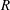$R$ is Cohen–Macaulay of arbitrary dimension and 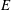$E$ is not necessarily of finite colength, and we notice a constraint in terms of the second analytic deviation of the module 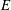$E$ if its reduction number is at least three.

Keywords

special fiber ringRees algebrareductionreduction numberanalytic spreadHilbert-Samuel multiplicityCohen-MacaulayGorensteinBuchsbaum-Rim multiplicity

MSC classification

Primary: 13A30: Associated graded rings of ideals (Rees ring, form ring), analytic spread and related topics
Secondary: 13H10: Special types (Cohen-Macaulay, Gorenstein, Buchsbaum, etc.) 13H15: Multiplicity theory and related topics 13A02: Graded rings 13C15: Dimension theory, depth, related rings (catenary, etc.) 13D40: Hilbert-Samuel and Hilbert-Kunz functions; Poincaré series 13E15: Rings and modules of finite generation or presentation; number of generators
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 1 , February 2020 , pp. 225 - 242
Copyright
© Canadian Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by CAPES-Brazil (grant 88881.121012/2016-01), and by CNPq-Brazil (grant 421440/2016-3).

References

Aberbach, I. M. and Huneke, C., An improved Briançon-Skoda theorem with applications to the Cohen–Macaulayness of Rees algebras . Math. Ann. 297(1993), 343–369. https://doi.org/10.1007/BF01459507.Google Scholar
Brennan, J., Ulrich, B., and Vasconcelos, W. V., The Buchsbaum-Rim polynomial of a module . J. Algebra 241(2001), 379–392. https://doi.org/10.1006/jabr.2001.8764.Google Scholar
Bruns, W. and Herzog, J., Cohen–Macaulay rings . Revised Edition. Cambridge University Press, Cambridge, 1998.Google Scholar
Buchsbaum, D. and Rim, D. S., A generalized Koszul complex. II. Depth and multiplicity . Trans. Amer. Math. Soc. 111(1964), 197–224. https://doi.org/10.2307/1994241.Google Scholar
Chan, C.-Y. J., Liu, J.-C., and Ulrich, B., Buchsbaum-Rim multiplicities as Hilbert-Samuel multiplicities . J. Algebra 319(2008), 4413–4425. https://doi.org/10.1016/j.jalgebra.2007.12.025.Google Scholar
Corso, A., Ghezzi, L., Polini, C., and Ulrich, B., Cohen–Macaulayness of special fiber rings . Comm. Algebra 31(2003), 3713–3734. https://doi.org/10.1081/AGB-120022439.Google Scholar
Corso, A., Polini, C., and Vasconcelos, W., Multiplicity of the special fiber of blowups . Math. Proc. Cambridge Philos. Soc. 140(2006), 207–219. https://doi.org/10.1017/S0305004105009023.Google Scholar
Cortadellas, T. and Zarzuela, S., On the structure of the fiber cone of ideals with analytic spread one . J. Algebra 317(2007), 759–785. https://doi.org/10.1016/j.jalgebra.2007.02.044.Google Scholar
D’ Cruz, C. and Verma, J. K., Hilbert series of fiber cones of ideals with almost minimal mixed multiplicity . J. Algebra 251(2002), 98–109. https://doi.org/10.1006/jabr.2001.9139.Google Scholar
Eisenbud, D. and Huneke, C., Cohen–Macaulay Rees algebras and their specialization . J. Algebra 81(1983), 202–224. https://doi.org/10.1016/0021-8693(83)90216-8.Google Scholar
Eisenbud, D., Huneke, C., and Ulrich, B., What is the Rees algebra of a module? Proc. Amer. Math. Soc. 131(2002), 701–708. https://doi.org/10.1090/S0002-9939-02-06575-9.Google Scholar
Goto, S., Hayasaka, F., Kurano, K., and Nakamura, Y., Rees algebras of the second syzygy module of the residue field of a regular local ring . Contemp. Math. 390(2005), 97–108. https://doi.org/10.1090/conm/390/07296.Google Scholar
Heinzer, W. and Kim, M.-K., Properties of the fiber cone of ideals in local rings . Comm. Algebra 31(2003), 3529–3546. https://doi.org/10.1081/AGB-120022240.Google Scholar
Huckaba, S. and Huneke, C., Rees algebras of ideals having small analytic deviation . Trans. Amer. Math. Soc. 339(1993), 373–402. https://doi.org/10.2307/2154225.Google Scholar
Huckaba, S. and Marley, T., Depth properties of Rees algebras and associated graded rings . J. Algebra 156(1993), 259–271. https://doi.org/10.1006/jabr.1993.1075.Google Scholar
Huckaba, S. and Marley, T., On associated graded rings of normal ideals . J. Algebra 222(1999), 146–163. https://doi.org/10.1006/jabr.1999.7985.Google Scholar
Huneke, C., On the associated graded ring of an ideal . Illinois J. Math. 26(1982), 121–137.Google Scholar
Huneke, C. and Sally, J., Birational extensions in dimension two and integrally closed ideals . J. Algebra 115(1988), 481–500. https://doi.org/10.1016/0021-8693(88)90274-8.Google Scholar
Huneke, C. and Swanson, I., Integral closure of ideals, rings and modules . London Math. Soc. Lecture Note Ser., 336. Cambridge University Press, Cambridge, 2006.Google Scholar
Jayanthan, A. V., Puthenpurakal, T. J., and Verma, J. K., On fiber cones of  $\mathfrak{m}$ -primary ideals. Canad. J. Math. 59(2007), 109–126. https://doi.org/10.4153/CJM-2007-005-8.Google Scholar
Korb, T. and Nakamura, Y., On the Cohen–Macaulayness of multi-Rees algebras and Rees algebras of powers of ideals . J. Math. Soc. Japan 50(1998), 451–467. https://doi.org/10.2969/jmsj/05020451.Google Scholar
Kurano, K., On Macaulayfication obtained by a blow-up whose center is an equi-multiple ideal . J. Algebra 190(1997), 405–434. https://doi.org/10.1006/jabr.1996.6904.Google Scholar
Lima, P. H. and Jorge Pérez, V. H., On the Gorenstein property of the fiber cone to filtration . Int. J. Algebra 8(2014), 159–174. https://doi.org/10.12988/ija.2014.312135.Google Scholar
Lin, K.-N. and Polini, C., Rees algebras of truncations of complete intersections . J. Algebra 410(2014), 36–52. https://doi.org/10.1016/j.jalgebra.2014.03.022.Google Scholar
Lipman, J., Cohen–Macaulayness in graded algebras . Math. Res. Lett. 1(1994), 149–157. https://doi.org/10.4310/MRL.1994.v1.n2.a2.Google Scholar
Miranda-Neto, C. B., Graded derivation modules and algebraic free divisors . J. Pure Appl. Algebra 219(2015), 5442–5466. https://doi.org/10.1016/j.jpaa.2015.05.026.Google Scholar
Miranda-Neto, C. B., On Aluffi’s problem and blowup algebras of certain modules . J. Pure Appl. Algebra 221(2017), 799–820. https://doi.org/10.1016/j.jpaa.2016.08.004.Google Scholar
Ooishi, A., On the Gorenstein property of the associated graded ring and the Rees algebra of an ideal . J. Algebra 155(1993), 397–414. https://doi.org/10.1006/jabr.1993.1051.Google Scholar
Polini, C. and Ulrich, B., Necessary and sufficient conditions for the Cohen–Macaulayness of blowup algebras . Compos. Math. 119(1999), 185–207. https://doi.org/10.1023/A:1001704003619.Google Scholar
Polini, C. and Xie, Y., j-multiplicity and depth of associated graded modules . J. Algebra 379(2013), 31–49. https://doi.org/10.1016/j.jalgebra.2013.01.001.Google Scholar
Sancho de Salas, J. B., Blowing-up morphisms with Cohen–Macaulay associated graded rings . In: Géométrie algébrique et applications, I . Travaux en Cours, 22. Hermann, Paris, 1987, pp. 201–209.Google Scholar
Shah, K., On the Cohen–Macaulayness of the fiber cone of an ideal . J. Algebra 143(1991), 156–172. https://doi.org/10.1016/0021-8693(91)90257-9.Google Scholar
Simis, A., Ulrich, B., and Vasconcelos, W., Rees algebras of modules . Proc. London Math. Soc. 87(2003), 610–646. https://doi.org/10.1112/S0024611502014144.Google Scholar
Trung, N. V. and Ikeda, S., When is the Rees algebra Cohen–Macaulay? Comm. Algebra 17(1989), 2893–2922. https://doi.org/10.1080/00927878908823885.Google Scholar
Trung, N. V., Viet, D. Q., and Zarzuela, S., When is the Rees algebra Gorenstein? J. Algebra 175(1995), 137–156. https://doi.org/10.1006/jabr.1995.1179.Google Scholar
Vasconcelos, W. V., Arithmetic of blowup algebras . London Math. Soc. Lecture Note Ser., 195, Cambridge University Press, Cambridge, 1994. https://doi.org/10.1017/CBO9780511574726.Google Scholar
Vasconcelos, W. V., Integral closure. Rees algebras, multiplicities, algorithms . Springer Monographs on Mathematics. Springer-Verlag, Berlin, 2005.Google Scholar
Viet, D. Q., On the multiplicity and the Cohen–Macaulayness of fiber cones of graded algebras . J. Pure Appl. Algebra 213(2009), 2104–2116. https://doi.org/10.1016/j.jpaa.2009.03.006.Google Scholar