Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:34:26.379Z Has data issue: false hasContentIssue false
  • English
  • Français

On Some Relations Between Partial and Ordinary Differential Equations

Published online by Cambridge University Press:  20 November 2018

Erwin Kreyszig
Erwin Kreyszig*
Affiliation:
University of Ottawa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theory of solutions of partial differential equations

(1.1)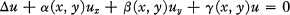 with analytic coefficients can be based upon the theory of analytic functions of a complex variable; the basic tool in this approach is integral operators which map the set of solutions of (1.1) onto the algebra of analytic functions. For certain classes of operators this mapping which is first defined in the small, can be continued to the large, cf. Bergman (3).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 10 , 1958 , pp. 183 - 190
Copyright
Copyright © Canadian Mathematical Society 1958

References

1. Bergman, S., Ueber Kurvenintegrale von Funktionen zweier komplexer Veraenderlicher, die die Differentialgleichung ΔV + 7 = 0 befriedigen, Math. Z. 32 (1930), 386-405.Google Scholar
2. Bergman, S., Zur Théorie der Funktionen, die eine lineare partielle Differentialgleichung befriedigen, Rec. Math. (Mat. Sbornik) N.S. 2 (1937), 1169–1198.Google Scholar
3. Bergman, S., Linear operators in the theory of partial differential equations, Trans. Amer. Math. Soc. 58 (1943), 130-155. Google Scholar
4. Kreyszig, E., On a class of partial differential equations, J. Rat. Mech. Anal. 4 (1955), 907-923.Google Scholar
5. Kreyszig, E., On certain partial differential equations and their singularities, J. Rat. Mech. Anal. 5 (1956), 805-820.Google Scholar
6. Hadamard, J., Essai sur l'étude des fonctions données par leur développement de Taylor, J. de Math. pur. appl. (4) 8 (1892), 101-186.Google Scholar