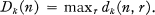Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Erdös, Paul
1970.
On Sets of Distances of n Points.
The American Mathematical Monthly,
Vol. 77,
Issue. 7,
p.
738.
Erdös, Paul
and
Purdy, George
1971.
Some extremal problems in geometry.
Journal of Combinatorial Theory, Series A,
Vol. 10,
Issue. 3,
p.
246.
Erdós, P.
Meir, A.
Sós, V.T.
and
Turán, P.
1972.
On some applications of graph theory, I.
Discrete Mathematics,
Vol. 2,
Issue. 3,
p.
207.
Purdy, George
1974.
Some external problems in geometry.
Discrete Mathematics,
Vol. 7,
Issue. 3-4,
p.
305.
Erdös, Paul
1977.
Paul turán, 1910–1976: His work in graph theory.
Journal of Graph Theory,
Vol. 1,
Issue. 2,
p.
97.
Erdös, P.
1985.
PROBLEMS AND RESULTS IN COMBINATORIAL GEOMETRYa.
Annals of the New York Academy of Sciences,
Vol. 440,
Issue. 1,
p.
1.
Erdős, P.
and
Pach, J.
1990.
Variations on the theme of repeated distances.
Combinatorica,
Vol. 10,
Issue. 3,
p.
261.
Pach, János
and
Sharir, Micha
1992.
Repeated angles in the plane and related problems.
Journal of Combinatorial Theory, Series A,
Vol. 59,
Issue. 1,
p.
12.
1995.
Combinatorial Geometry.
p.
319.
Erdös, P.
Meir, A.
Sós, V.T.
and
Turán, P.
2006.
On some applications of graph theory, I.
Discrete Mathematics,
Vol. 306,
Issue. 10-11,
p.
853.
Swanepoel, Konrad J.
2009.
Unit Distances and Diameters in Euclidean Spaces.
Discrete & Computational Geometry,
Vol. 41,
Issue. 1,
p.
1.
Swanepoel, Konrad J.
2013.
Thirty Essays on Geometric Graph Theory.
p.
499.
Swanepoel, Konrad J.
2018.
New Trends in Intuitive Geometry.
Vol. 27,
Issue. ,
p.
407.
Simonovits, Miklós
and
Szemerédi, Endre
2019.
Building Bridges II.
Vol. 28,
Issue. ,
p.
445.
Alon, Noga
Bucić, Matija
and
Sauermann, Lisa
2025.
Unit and Distinct Distances in Typical Norms.
Geometric and Functional Analysis,
Vol. 35,
Issue. 1,
p.
1.