Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T12:47:33.306Z Has data issue: false hasContentIssue false
  • English
  • Français

On Self-Adjoint Factorization of Operators

Published online by Cambridge University Press:  20 November 2018

Heydar Radjavi
Heydar Radjavi*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main result of this paper is that every normal operator on an infinitedimensional (complex) Hilbert space ℋ is the product of four self-adjoint operators; our Theorem 4 is an actually stronger result. A large class of normal operators will be given which cannot be expressed as the product of three self-adjoint operators.

This work was motivated by a well-known resul t of Halmos and Kakutani (3) that every unitary operator on ℋ is the product of four symmetries, i.e., operators that are self-adjoint and unitary.

1. By “operator” we shall mean bounded linear operator. The space ℋ will be infinite-dimensional (separable or non-separable) unless otherwise specified. We shall denote the class of self-adjoint operators on ℋ by 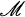and that of symmetries by .

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1421 - 1426
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Davis, Chandler, Separation of two linear subspaces, Acta. Sci. Math. (Szeged) 19 (1958), 172–187.Google Scholar
2. Halmos, P. R., A Hilbert space problem book (Van Nostrand, Princeton, N.J., 1967).Google Scholar
3. Halmos, P. R. and Kakutani, S., Products of symmetries, Bull. Amer. Math. Soc. 64 (1958), 77–78.Google Scholar
4. Radjavi, Heydar, Products of hermitian matrices and symmetries, Proc. Amer. Math. Soc. 21 (1969), 369–372.Google Scholar
5. Radjavi, Heydar and Williams, James, Products of self-adjoint operators, Michigan Math. J. 16 (1969), 177–185.Google Scholar