Let 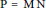$\text{P}\,\text{=}\,\text{M}\,\text{N}$ be a Levi decomposition of a maximal parabolic subgroup of a connected reductive group 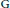$\text{G}$ over a 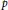$p$-adic field $F$. Assume that there exists 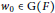${{w}_{0}}\,\in \,G\left( F \right)$ that normalizes 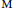$\text{M}$ and conjugates $\text{p}$ to an opposite parabolic subgroup. When 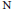$\text{N}$ has a Zariski dense 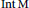$\text{Int}\,\text{M}$-orbit, $\text{F}$. Shahidi and $\text{X}$. Yu described a certain distribution 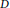$D$ on 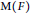$\text{M}\left( F \right)$, such that, for irreducible unitary supercuspidal representations $\pi $ of 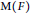$\text{M}\left( F \right)$ with 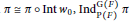$\pi \,\cong \,\pi \,\circ \,\text{Int}\,{{w}_{0}},\,\text{Ind}_{\text{P}\left( F \right)}^{\text{G}\left( F \right)}\,\pi $ is irreducible if and only if 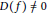$D\left( f \right)\,\ne \,0$ for some pseudocoefficient 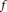$f$ of $\pi $. Since this irreducibility is conjecturally related to $\pi $ arising via transfer from certain twisted endoscopic groups of 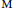$\text{M}$, it is of interest to realize 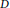$D$ as endoscopic transfer from a simpler distribution on a twisted endoscopic group 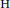$\text{H}$ of 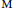$\text{M}$. This has been done in many situations where 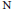$\text{N}$ is abelian. Here we handle the standard examples in cases where 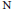$\text{N}$ is nonabelian but admit a Zariski dense 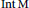$\text{Int}\,\text{M}$-orbit.