Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T01:04:20.203Z Has data issue: false hasContentIssue false
  • English
  • Français

On Representations of Orders Over Dedekind Domains

Published online by Cambridge University Press:  20 November 2018

D. G. Higman
D. G. Higman*
Affiliation:
University of Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study representations of o-orders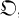, that is, of o-regular 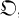-algebras, in the case that o is a Dedekind domain. Our main concern is with those 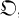-modules, called 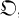-representation modules, which are regular as o-modules. For any 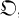-module M we denote by D(M) the ideal consisting of the elements x ∈ o such that x.Ext1(M, N) = 0 for all 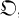-modules N, where Ext = Ext(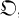,0) is the relative functor of Hochschild (5). To compute D(M) we need the small amount of homological algebra presented in § 1. In § 2 we show that the 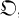-representation modules with rational hulls isomorphic to direct sums of right ideal components of the rational hull A of 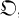, called principal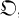-modules, are characterized by the property that D(M) ≠ 0. The (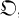, o)-projective 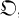-modules are those with D(M) = 0. We observe that D(M) divides the ideal I(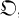) of (2) for every M , and give another proof of the fact that I(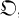) ≠ 0 if and only if A is separable. Up to this point, o can be taken to be an arbitrary integral domain.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 12 , 1960 , pp. 107 - 125
Copyright
Copyright © Canadian Mathematical Society 1960

References

1. Cartan, H. and Eilenberg, S., Homological algebra (Princeton, 1956).Google Scholar
2. Higman, D.G., On orders in separable algebras, Can. J. Math., 7 (1955), 509–515.Google Scholar
3. Cartan, H. and Eilenberg, S. Relative cohomology, Can. J. Math., 9 (1957), 19–34.Google Scholar
4. Higman, D.G. and MacLaughlin, J.E., Finiteness of class numbers of representations of algebras over function fields, to appear in the Michigan Journal of Mathematics.Google Scholar
5. Hochschild, G., Relative homological algebra, Trans. Amer. Math. Soc, 82 (1956), 246–269.Google Scholar
6. Maranda, J-M., On p-adic integral representations of finite groups, Can. J. Math., 5 (1953), 344–355.Google Scholar
7. Maranda, J-M. On the equivalence of representations of finite groups by groups of automorphisms of modules over Dedekind rings, Can. J. Math., 7 (1955), 516–526.Google Scholar
8. Reiner, I., Maschke modules over Dekedind rings, Can. J. Math., 8 (1956), 329–334.Google Scholar
9. Reiner, I. On class numbers of representations of an order, A. M. S. Notices, 5 (1958), Abstract no. 548-142, 584.Google Scholar