Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T18:53:19.798Z Has data issue: false hasContentIssue false
  • English
  • Français

On Reductive Lie Admissible Algebras

Published online by Cambridge University Press:  20 November 2018

Arthur A. Sagle
Arthur A. Sagle*
Affiliation:
University of Minnesota, Minneapolis, Minnesota
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Lie admissible algebra is a non-associative algebra A such that A− is a Lie algebra where A− denotes the anti-commutative algebra with vector space A and with commutation [X, Y] = XY – YX as multiplication; see [1; 2; 5]. Next let L−(X): A− → A−: Y → [X, Y] and H = {L−(X): X ∊ A−}; then, since A− is a Lie algebra, we see that H is contained in the derivation algebra of A− and consequently the direct sum g = A − ⊕ H can be naturally made into a Lie algebra with multiplication [PQ] given by: P = X + L−(U), Q = Y + L−(V) ∊ g, then

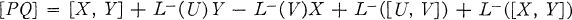
and note that for any P, [PP] = 0 so that [PQ] = −[QP] and the Jacobi identity for g follows from the fact that A− is Lie.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 2 , April 1971 , pp. 325 - 331
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Albert, A. A., Power associative rings, Trans. Amer. Math. Soc. 64 (1948), 552–593.Google Scholar
2. Coppage, W., Peirce decomposition in simple Lie admissible power associative algebras, Dissertation, Ohio State University, Columbus, Ohio, 1963.Google Scholar
3. Jacobson, N., Lie algebras, Interscience Tracts in Pure and Applied Mathematics, No. 10 (Interscience, a division of Wiley, New York-London, 1962).Google Scholar
4. Jenner, W. E., Truncation algebras, Notices Amer. Math. Soc. Abstract 672-50 17 (1970), 98.Google Scholar
5. Laufer, P. J. and Tomber, M. L., Some Lie admissible algebras, Can. J. Math. 14 (1962), 287–292.Google Scholar
6. Sagle, A., Malcev algebras, Trans. Amer. Math. Soc. 101 (1961), 426–458.Google Scholar
7. Sagle, A., On anti-commutative algebras and general Lie triple systems, Pacific J. Math. 15 (1965), 281–291.Google Scholar
8. Sagle, A., A note on triple systems and totally geodesic submanifolds in a homogeneous space, Nagoya Math. J. 32 (1968), 5–20 (in particular, § 5).Google Scholar
9. Sagle, A. and Winter, D., On homogeneous spaces and reductive subalgebras of simple Lie algebras, Trans. Amer. Math. Soc. 128 (1967), 142–147.Google Scholar
10. Yamaguti, K., Note on Malcev algebras, Kumamoto J. Sci. 5 (1962), 203–207.Google Scholar
11. Yamaguti, K., On the theory of Malcev algebras, Kumamoto J. Sci. 6 (1963), 9–45.Google Scholar