Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:36:47.593Z Has data issue: false hasContentIssue false
  • English
  • Français

On Quasi-Essential Subgroups of Primary Abelian Groups

Published online by Cambridge University Press:  20 November 2018

Khalid Benabdallah  and
John M. Irwin
Khalid Benabdallah
Affiliation:
Université de Montréal, Montréal, Québec;
John M. Irwin
Affiliation:
Université de Montréal, Montréal, Québec; Wayne State University. Detroit, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All groups considered in this paper are abelian. A subgroup N of a group G is said to be a quasi-essential subgroup of G if G = 〈H, K〉 whenever H is an N-high subgroup of G and K is a pure subgroup of G containing N. We started the study of such subgroups in [5]; in particular, we characterized subsocles of a primary group which were both quasi-essential and centres of purity. In this paper we show that quasi-essential subsocles of a primary group are necessarily centres of purity answering thus in the affirmative a question raised in [5].

We obtain the following theorem: A subsocle S of a p-group G is quasi-essential if and only if either S ⊂ G1or (pnG)[p] ⊃ S ⊃ (pn+1G)[p] for some non-negative integer n. The notation is that of [1]. If G is a group, then

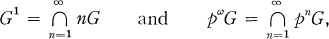
where p is a prime integer.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 6 , 01 December 1970 , pp. 1176 - 1184
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Fuchs, L., Abelian groups (Publishing House of the Hungarian Academy of Sciences, Budapest, 1958).Google Scholar
2. Hill, P., On quasi-isomorphic invariants of primary groups. Pacific J. Math. 22 (1967), 257–265.Google Scholar
3. Hill, P. and Megibben, C., Minimal pure subgroups in primary groups, Bull. Soc. Math. France 92 (1964), 251–257.Google Scholar
4. Irwin, J. M., High subgroups of Abelian torsion groups, Pacific J. Math. 11 (1961), 1375–1384.Google Scholar
5. Irwin, J. M. and Benabdallah, K., On N-high subgroups of Abelian groups, Bull. Soc. Math. France 96 (1968), 337–346.Google Scholar
6. Irwin, J. M. and Walker, E. A., On N-high subgroups of Abelian groups, Pacific J. Math. 11 (1961), 1375–1384.Google Scholar
7. Irwin, J. M., Richman, F., and Walker, E. A., Countable direct sums of torsion complete groups, Proc. Amer. Math. Soc. 17 (1966), 763–766.Google Scholar
8. Kaplansky, I., Infinite abelian groups (University of Michigan Press, Ann Arbor, 1954).Google Scholar
9. Megibben, C. and Hill, P., Quasi-closed primary groups, Acta Math. Acad. Sci. Hungar. 16 (1965), 271–274.Google Scholar
10. Mitchell, R., Some properties of basic and semi-basic subgroups, Ph.D. Dissertation, New Mexico State University, Las Cruces, New Mexico, 1964.Google Scholar
11. Pierce, R. S., Centers of purity in Abelian groups, Pacific J. Math3 18 (1963), 215–219.Google Scholar
12. Reid, J. D., On subgroups of an Abelian group maximal disjoint from a given subgroup- Pacific J. Math. 13 (1963), 657–663.Google Scholar