The following problem has been suggested by Paul Turán. Let 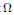$\Omega $ be a symmetric convex body in the Euclidean space 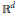${{\mathbb{R}}^{d}}$ or in the torus 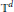${{\mathbb{T}}^{d}}$. Then, what is the largest possible value of the integral of positive definite functions that are supported in 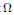$\Omega $ and normalized with the value 1 at the origin? From this, Arestov, Berdysheva and Berens arrived at the analogous pointwise extremal problem for intervals in 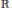$\mathbb{R}$. That is, under the same conditions and normalizations, the supremum of possible function values at 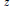$z$ is to be found for any given point 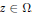$z\,\in \,\Omega $. However, it turns out that the problem for the real line has already been solved by Boas and Kac, who gave several proofs and also mentioned possible extensions to 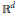${{\mathbb{R}}^{d}}$ and to non-convex domains as well.

Here we present another approach to the problem, giving the solution in 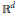${{\mathbb{R}}^{d}}$ and for several cases in 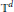${{\mathbb{T}}^{d}}$. Actually, we elaborate on the fact that the problem is essentially one-dimensional and investigate non-convex open domains as well. We show that the extremal problems are equivalent to some more familiar ones concerning trigonometric polynomials, and thus find the extremal values for a few cases. An analysis of the relationship between the problem for 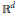${{\mathbb{R}}^{d}}$ and that for 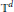${{\mathbb{T}}^{d}}$ is given, showing that the former case is just the limiting case of the latter. Thus the hierarchy of difficulty is established, so that extremal problems for trigonometric polynomials gain renewed recognition.