No CrossRef data available.
Article contents
On Partitions into Powers of Primes and Their Difference Functions
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper, we extend the approach first outlined by Hardy and Ramanujan for calculating the asymptotic formulae for the number of partitions into 
$r$-th powers of primes, 
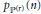${{p}_{\mathbb{P}\left( r \right)}}\left( n \right)$, to include their difference functions. In doing so, we rectify an oversight of said authors, namely that the first difference function is perforce positive for all values of 
$n$, and include the magnitude of the error term.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
[1]
Bateman, P. T. and Erdös, P., Partitions into primes.
Publ. Math. Debrecen
4(1956), 198–200.Google Scholar
[2]
Bateman, P. T. and Erdös, P., Monotonicity of partition functions.
Mathematika
3(1956), 1–14.Google Scholar
[4]
Gupta, H., Products of parts in partitions into primes.
Res. Bull. Panjab. Univ. (N. S.)
21(1970), 251–253.Google Scholar
[5]
Hardy, G. H. and Ramanujan, S., Asymptotic formulae for the distribution of integers of various types.
Proc. London Math. Soc. (2)
16(1917), 112–132.Google Scholar
[6]
Kerawala, S. M., On the asymptotic values of
ln p A (n ) and ln p (d ) A (n ) with A as the set of primes. J. Natur. Sci. and Math. 9(1969), 209–216.Google Scholar
[7]
Mitsui, T., On the partitions of a number into the powers of prime numbers.
J. Math. Soc. Japan
9(1957), 428–447.Google Scholar
You have
Access