Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wilker, J. B.
1977.
Sizing up a solid packing.
Periodica Mathematica Hungarica,
Vol. 8,
Issue. 2,
p.
117.


 is packed in order of decreasing diameters into the unit cube
is packed in order of decreasing diameters into the unit cube 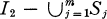 has an asymptotic lower bound
has an asymptotic lower bound 