Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-19T11:47:30.310Z Has data issue: false hasContentIssue false
  • English
  • Français

On Open Projections of GCR Algebras

Published online by Cambridge University Press:  20 November 2018

Trond Digernes  and
Herbert Halpern
Trond Digernes
Affiliation:
University of Oslo, Oslo, Norway
Herbert Halpern
Affiliation:
University of Cincinnati Cincinnati, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper 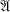will denote a C*-algebra and 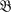will denote its second dual, which is identified with the enveloping von Neumann algebra of 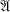. A projection E in 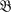is said to be open if it supports a left ideal in 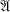, that is, if 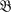E = 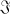- for some left ideal 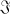in 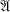. Here the bar - means the stong closure. When 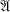has a unit, this definition coincides with the definition of Akemann [1, Definition II. 1]. In the sequel, we shall solely be concerned with two-sided ideals, and consequently central projections [4, I, § 3, Corollary 3 of Theorem 2]. Our aim is to show that 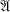is CCR if and only if the open central projections are strongly dense in the set of central projections on .

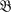Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 5 , October 1972 , pp. 978 - 982
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Akemann, C., The general Stone-Weierestrass problem, J. Functional Analysis 4 (1969), 277–294.Google Scholar
2. Bade, W. G., On Boolean algebras of projections and algebras of operators, Trans. Amer. Math. Soc. 80 (1955), 345–360.Google Scholar
3. Dixmier, J., Les C*-algebres et leurs representations (Gauthier-Villars, Paris, 1964).Google Scholar
4. Dixmier, J., Les algebres d'operateurs dans l’espace Hilbertien (Gauthier-Villars, Paris, 2e édition, 1969).Google Scholar
5. Elliott, G., Ideal preserving automorphisms of postliminary C*-algebras, Proc. Amer. Math. Soc. 27 (1971), 107–109.Google Scholar
6. Halpern, H., A generalized dual for a C*-algebra, Trans. Amer. Math. Soc. 153 (1971), 139–156.Google Scholar
7. Lance, E., Automorphisms of postliminary C*-algebras, Pacific J. Math. 23 (1967), 547–555.Google Scholar