Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T03:04:36.995Z Has data issue: false hasContentIssue false
  • English
  • Français

On Non-Archimedean Curves Omitting Few Components and their Arithmetic Analogues

Published online by Cambridge University Press:  20 November 2018

Aaron Levin  and
Julie Tzu-Yueh Wang
Aaron Levin
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824 e-mail: [email protected]
Julie Tzu-Yueh Wang
Affiliation:
Institute of Mathematics, Academia Sinica, No. 1, Sec., Roosevelt Road, Taipei 10617, TAIWAN e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\mathbf{k}$ be an algebraically closed field complete with respect to a non-Archimedean absolute value of arbitrary characteristic. Let 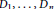${{D}_{1}},...,\,{{D}_{n}}$ be effective nef divisors intersecting transversally in an $n$-dimensional nonsingular projective variety $X$. We study the degeneracy of non-Archimedean analytic maps from $\mathbf{k}$ into 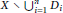$X\,\backslash \,\cup _{i=1}^{n}\,{{D}_{i}}$ under various geometric conditions. When $X$ is a rational ruled surface and 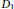${{D}_{1}}$ and 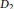${{D}_{2}}$ are ample, we obtain a necessary and sufficient condition such that there is no non-Archimedean analytic map from $\mathbf{k}$ into 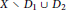$X\,\backslash \,{{D}_{1}}\,\cup \,{{D}_{2}}$. Using the dictionary between non-Archimedean Nevanlinna theory and Diophantine approximation that originated in earlier work with T. T. H. An, we also study arithmetic analogues of these problems, establishing results on integral points on these varieties over $\mathbb{Z}$ or the ring of integers of an imaginary quadratic field.

Keywords

11J9732P0532H25non-Archimedean Picard theoremnon-Archimedean analytic curvesintegral points
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 1 , 01 February 2017 , pp. 130 - 142
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] An, T. T. H., A defect relation for non-Archimedean analytic curves in arbitrary projective varieties. Proc. Amer. Math. Soc. 135(2007), 1255–1261. http://dx.doi.org/10.1090/S0002-9939-06-08591-1 Google Scholar
[2] An, T. T. H., Levin, A., and J. Wang, T.-Y. A p-adic Nevanlinna-Diophantine correspondence. Acta Arith. 146(2011), no. 4, 379–397. http://dx.doi.Org/10.4064/aa146-4-5 Google Scholar
[3] An, T. T. H., Wang, J. T.-Y., and Wong, P.-M., Non-Archimedean analytic curves in the complements of hypersurface divisors. J. Number Theory 128(2008), no. 8, 2275–2281.http://dx.doi.Org/10.1016/j.jnt.2007.10.011 Google Scholar
[4] Fulton, W., Intersection theory. Second rd., Ergebnisse der Mathematik und ihrer Grenzgebiete, 3, Springer-Verlag, Berlin, 1998.Google Scholar
[5] Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, NewYork, 1977.Google Scholar
[6] Kleiman, S. L., Toward a numerical theory of ampleness. Ann. of Math. 84(1966), 293–344.http://dx.doi.org/10.2307/1970447 Google Scholar
[7] Kollár, J., Rational curves on algebraic varieties. Ergebnisse der Mathematik und ihrer Grenzgebiete, 32, Springer-Verlag, Berlin, 1996.Google Scholar
[8] Lazarsfeld, R., Positivity in algebraic geometry. I. Classical setting: line bundles and linear series. A Series of Modern Surveys in Mathematics vol. 48, Springer-Verlag, Berlin, 2004.Google Scholar
[9] Levin, A., Variations on a theme ofRunge: effective determination of integral points on certain varieties. J. Théor. Nombres Bordeaux 20(2008), no. 2, 385–417. http://dx.doi.Org/10.5802/jtnb.634 Google Scholar
[10] Lin, C.-W. and Wang, J. T.-Y., Generalizations of rigid analytic Picard theorems. Proc. Amer. Math. Soc. 138(2010), 133–139. http://dx.doi.org/10.1090/S0002-9939-09-10038-2 Google Scholar
[11] Matsusaka, T., On numerically effective divisors with positive self-intersection numbers. J. Fac. Sci. Univ. Tokyo 38(1991), no. 1,165–183.Google Scholar
[12] Serre, J.-P., Lectures on the Mordell-Weil theorem. In: Aspects of Mathematics, third ed., Friedr.Vieweg & Sohn, Braunschweig, 1997.Google Scholar
[13] Vojta, P., Diophantine approximations and value distribution theory. Lecture Notes in Mathematics, 1239, Springer-Verlag, Berlin, 1987.Google Scholar