Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T01:33:37.705Z Has data issue: false hasContentIssue false
  • English
  • Français

On Multipliers with Unconditionally Converging Fourier Series

Published online by Cambridge University Press:  20 November 2018

Gregory F. Bachelis  and
Louis Pigno
Gregory F. Bachelis
Affiliation:
Kansas State University, Manhattan, Kansas
Louis Pigno
Affiliation:
Kansas State University, Manhattan, Kansas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a compact abelian group with dual group Γ. For 1 ≦ p < ∞, 1 ≦ q < ∞, let 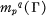denote the Banach space of complex-valued functions on Γ which are multipliers of type (p, q) and 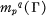the subspace of compact multipliers.

Grothendieck [10; 11] has proven that a function in LP(G), 1 ≦ p < 2, has an unconditionally converging Fourier series in LP(G) if and only if it is in L2(G), and Helgason [12] has proven that the derived algebra of LP(G), 1 ≦ p < 2, is L2(G). Using these results we show in § 2 that a multiplier of type (p, g), 1 ≦ p ≦ 2, 1 ≦ q ≦ 2, has an unconditionally converging Fourier series in 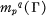if and only if it is in 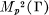(Theorem 2.1), and that, for 1 ≦ p ≦ q ≦ 2, the derived algebra of 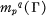is 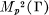(Theorem 2.2). Statements equivalent to the above are also given.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 3 , June 1972 , pp. 477 - 484
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Bachelis, G. F., On the ideal of unconditionally convergent Fourier series in LP(G), Proc. Amer. Math. Soc. 27 (1971), 309–312.Google Scholar
2. Bachelis, G. F. and Gilbert, J. E., Banach spaces of compact multipliers and their dual spaces (to appear in Math. Z.).Google Scholar
3. Bachelis, G. F. and Rosenthal, H. P., On unconditionally converging series and biorthogonal systems in a Banach space, Pacific J. Math. 37 (1971), 1–5.Google Scholar
4. Day, M. M., Normed linear spaces (Academic Press, New York, 1962).Google Scholar
5. Edwards, R. E., Changing signs of Fourier coefficients, Pacific J. Math. 15 (1965), 463–475.Google Scholar
6. Edwards, R. E., Fourier series: a modern introduction, Vol. II (Holt, Rinehart and Winston, New York, 1967).Google Scholar
7. Figà-Talamanca, A. and Gaudry, G., Multipliers of Lp which vanish at infinity, J. Functional Analysis 7 (1971). 475–486.Google Scholar
8. Gaudry, G., Quasi-measures and multiplier problems, Ph.D. thesis, Australian National University, Canberra, 1965.Google Scholar
9. Gaudry, G., Bad behavior and inclusion results for multipliers of type (p, q), Pacific J. Math. 35 (1970), 83–93.Google Scholar
10. Grothendieck, A., Resultats nouveaux dans la theorie des operations lineaires., C. R. Acad. Sci. Paris (1954), 577–579.Google Scholar
11. Grothendieck, A., Resume de la theorie metrique des produits tensoriels topologiques, Bol. Soc. Mat. São Paulo 8 (1956), 1–79.Google Scholar
12. Helgason, S., Multipliers of Banach algebras, Ann. of Math. 64 (1956), 240–254.Google Scholar
13. Hewitt, E. and Ross, K., Abstract harmonic analysis, Vol. II (Springer, New York, 1970).Google Scholar
14. Hormander, L., Estimates for translation invariant operators in Lp spaces, Acta Math. 104 (1960), 93–140.Google Scholar
15. Lions, J.-L. and Peetre, J., Sur une classe d'espaces d'interpolation, Inst. Hautes Études Sci. Publ. Math. 19 (1964), 5–68.Google Scholar
16. Peyriere, J. and Spector, R., Sur les multiplicateurs radiaux de LP(G), pour un groupe abelien localement compact totalement discontinu, C. R. Acad. Sci. Paris Ser. A 269 (1969), 973–974.Google Scholar
17. Rudin, W., Fourier analysis on groups (Interscience, New York, 1962).Google Scholar
18. Zygmund, A., Trigonometric series, Vol. II (Cambridge University Press, Cambridge, 1959).Google Scholar