Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T12:51:10.164Z Has data issue: false hasContentIssue false
  • English
  • Français

On Morita Duality

Published online by Cambridge University Press:  20 November 2018

Bruno J. Mùller
Bruno J. Mùller*
Affiliation:
McMaster University, Hamilton, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

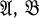A contra variant category-equivalence between categories of right R-modules and left S-modules (all rings have units, all modules are unitary) that contain RR, SS and are closed under submodules and factor modules, is naturally equivalent to a functor Horn (–, U) with a bimodule SUR such that SU, UR are injective cogenerators with S = End UR and R = End SU, and all modules in are [U-reflexive. Conversely, for any SSUR, Hom(–, U) is a contravariant category equivalence between the categories of [U-reflexive modules, and if U has the properties just stated, then these categories are closed under submodules, factor modules, and finite direct sums and contain RR, UR,SS, and SU. Such a functor will be called a (Morita) duality between R and S induced by U (see (5)).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1338 - 1347
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Azumaya, G., A duality theory for injective modules, Amer. J. Math. 81 (1959), 249–278.Google Scholar
2. Chandler, R. E. and Koh, K., Applications of a function topology on rings with unit, Illinois J. Math. 11 (1967), 580–585.Google Scholar
3. Lambek, J., Lectures on rings and modules (Blaisdell, Waltham, Massachusetts, 1966).Google Scholar
4. Matlis, E., Injective modules over Noetherian rings, Pacific J. Math. 8 (1958), 511–528.Google Scholar
5. Morita, K., Duality for modules and its applications to the theory of rings with minimum condition, Sci. Rep. Tokyo Kyoiku Daigaku Sect. A 6 (1958), 83–142.Google Scholar
6. Nagata, M., Local rings, Interscience Tracts in Pure and Applied Mathematics, No. 13 (Interscience, New York, 1962).Google Scholar
7. Osofsky, B. L., A generalization of quasi-Frobenius rings, J. Algebra 4 (1966), 373–387.Google Scholar
8. Rosenberg, A. and Zelinsky, D., Finiteness of the infective hull, Math. Z. 70 (1959), 372–380.Google Scholar
9. Rosenberg, A. and Zelinsky, D., Annihilators, Portugal. Math. 20 (1961), 53–65.Google Scholar