No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let 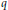 $q$ be an algebraic integer of degree
$q$ be an algebraic integer of degree 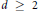 $d\ge 2$. Consider the rank of the multiplicative subgroup of
$d\ge 2$. Consider the rank of the multiplicative subgroup of 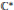 ${{\mathbb{C}}^{*}}$ generated by the conjugates of
${{\mathbb{C}}^{*}}$ generated by the conjugates of 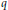 $q$. We say
$q$. We say 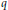 $q$ is of full rank if either the rank is
$q$ is of full rank if either the rank is 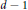 $d-1$ and
$d-1$ and 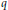 $q$ has norm
$q$ has norm 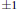 $\pm 1$, or the rank is
$\pm 1$, or the rank is 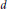 $d$. In this paper we study some properties of
$d$. In this paper we study some properties of 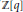 $\mathbb{Z}[q]$ where
$\mathbb{Z}[q]$ where 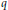 $q$ is an algebraic integer of full rank. The special cases of when
$q$ is an algebraic integer of full rank. The special cases of when 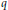 $q$ is a Pisot number and when
$q$ is a Pisot number and when 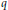 $q$ is a Pisot-cyclotomic number are also studied. There are four main results.
$q$ is a Pisot-cyclotomic number are also studied. There are four main results.
(1) If 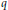 $q$ is an algebraic integer of full rank and
$q$ is an algebraic integer of full rank and  $n$ is a fixed positive integer, then there are only finitely many
$n$ is a fixed positive integer, then there are only finitely many 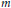 $m$ such that
$m$ such that 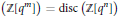 $\text{disc}\left( \mathbb{Z}\left[ {{q}^{m}} \right] \right)=\text{disc}\left( \mathbb{Z}\left[ {{q}^{n}} \right] \right)$.
$\text{disc}\left( \mathbb{Z}\left[ {{q}^{m}} \right] \right)=\text{disc}\left( \mathbb{Z}\left[ {{q}^{n}} \right] \right)$.
(2) If 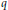 $q$ and
$q$ and  $r$ are algebraic integers of degree
$r$ are algebraic integers of degree 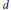 $d$ of full rank and
$d$ of full rank and 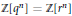 $\mathbb{Z}[{{q}^{n}}]=\mathbb{Z}[{{r}^{n}}]$ for infinitely many
$\mathbb{Z}[{{q}^{n}}]=\mathbb{Z}[{{r}^{n}}]$ for infinitely many  $n$, then either
$n$, then either 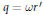 $q=\omega {r}'$ or
$q=\omega {r}'$ or 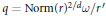 $q=\text{Norm}{{(r)}^{2/d}}\omega /r'$ , where
$q=\text{Norm}{{(r)}^{2/d}}\omega /r'$ , where 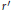 $r'$ is some conjugate of
$r'$ is some conjugate of  $r$ and
$r$ and 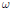 $\omega $ is some root of unity.
$\omega $ is some root of unity.
(3) Let  $r$ be an algebraic integer of degree at most 3. Then there are at most 40 Pisot numbers
$r$ be an algebraic integer of degree at most 3. Then there are at most 40 Pisot numbers 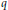 $q$ such that
$q$ such that 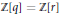 $\mathbb{Z}[q]=\mathbb{Z}[r]$.
$\mathbb{Z}[q]=\mathbb{Z}[r]$.
(4) There are only finitely many Pisot-cyclotomic numbers of any fixed order.
Please note a has been issued for this article.