Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:39:12.188Z Has data issue: false hasContentIssue false
  • English
  • Français

On Metanilpotent Varieties of Groups

Published online by Cambridge University Press:  20 November 2018

Narain Gupta
Narain Gupta*
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 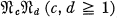denote the variety of all groups which are extensions of a nilpotent-of-class-c group by a nilpotent-of-class-d group, and let 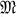denote the variety of all metabelian groups. The main result of this paper is the following theorem.

THEOREM. Let 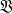be a subvariety of 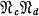which does not contain 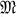. Then every 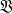-group is an extension of a group of finite exponent by a nilpotent group by a group of finite exponent. In particular, a finitely generated torsion-free 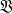-group is a nilpotent-by-finite group.

This generalizes the main theorem of Ŝmel′kin [4], where the same result is proved for subvarieties of 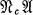, where 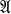is the variety of abelian groups. See also Lewin and Lewin [2] for a related discussion.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 4 , 01 August 1970 , pp. 875 - 877
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Gupta, N. D., Newman, M. F., and Tobin, S. J., On metabelian groups of prime-power exponent, Proc. Roy. Soc. Ser. A 302 (1968), 237–242.Google Scholar
2. Jacques, Lewin and Tekla Lewin, , Semigroup laws in varieties of solvable groups, Proc. Cambridge Philos. Soc. 65 (1969), 1–9.Google Scholar
3. Hanna, Neumann, Varieties of groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 37 (Springer-Verlag, New York, 1967).Google Scholar
4. Smel'kin, A. L., On soluble group mrieties, Soviet Math. Dokl. 9 (1968), 100–103. (English translation)Google Scholar