Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Handelman, D.
1974.
Prime regular rings of quotients.
Communications in Algebra,
Vol. 2,
Issue. 6,
p.
525.
Goldman, Oscar
1975.
Elements of noncommutative arithmetic I.
Journal of Algebra,
Vol. 35,
Issue. 1-3,
p.
308.
Beachy, John A.
1975.
On maximal torsion radicals. III.
Proceedings of the American Mathematical Society,
Vol. 52,
Issue. 1,
p.
113.
Papp, Zoltán
1975.
On stable noetherian rings.
Transactions of the American Mathematical Society,
Vol. 213,
Issue. 0,
p.
107.
Beachy, John A.
1976.
Noncommutative Ring Theory.
Vol. 545,
Issue. ,
p.
2.
Beachy, John A.
1978.
Injective modules with both ascending and descending chain conditions on annihilators.
Communications in Algebra,
Vol. 6,
Issue. 17,
p.
1777.
Herden, Gerhard
1980.
The lattice (,⊂) of arbitrary torsion classes for mod-r.
Communications in Algebra,
Vol. 8,
Issue. 15,
p.
1469.
Beachy, John A.
1982.
Advances in Non-Commutative Ring Theory.
Vol. 951,
Issue. ,
p.
41.
Meijer, A.R.
and
Smith, P.F.
1984.
The complement of Gabriel topologies.
Journal of Pure and Applied Algebra,
Vol. 31,
Issue. 1-3,
p.
119.
Evans, M. W.
1986.
Torsion theories over semihereditary rings.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 40,
Issue. 1,
p.
54.
Zhang, Binlong
1987.
Rings having thb ascbnding chain condition 1 with respect to a torsion radical.
Communications in Algebra,
Vol. 15,
Issue. 6,
p.
1205.
van den Berg, John E.
1999.
TORSION PRERADICALS—A TOOL FOR ANALYSING RINGS.
Quaestiones Mathematicae,
Vol. 22,
Issue. 3,
p.
465.
Beachy, John A.
2002.
M-INJECTIVE MODULES AND PRIMEM-IDEALS.
Communications in Algebra,
Vol. 30,
Issue. 10,
p.
4649.
Pérez, Jaime Castro
Raggi, Francisco
Montes, José Ríos
and
Berg, John van den
2005.
On the Atomic Dimension in Module Categories.
Communications in Algebra,
Vol. 33,
Issue. 12,
p.
4679.
Beachy, John A.
2016.
On Maximal Torsion Radicals, IV.
Communications in Algebra,
Vol. 44,
Issue. 3,
p.
1181.
Kanda, Ryo
2019.
Finiteness of the number of minimal atoms in Grothendieck categories.
Journal of Algebra,
Vol. 527,
Issue. ,
p.
182.
Kanda, Ryo
2022.
Integrality of noetherian Grothendieck categories.
Journal of Algebra,
Vol. 592,
Issue. ,
p.
233.


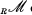 denote the category of unital left
denote the category of unital left 