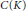Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Smith, Richard J.
and
Troyanski, Stanimir
2010.
Renormings of C(K) spaces.
Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas,
Vol. 104,
Issue. 2,
p.
375.
Cascales, Bernardo
and
Orihuela, José
2014.
Recent Progress in General Topology III.
p.
93.
Guirao, Antonio J.
Montesinos, Vicente
and
Zizler, Václav
2016.
Open Problems in the Geometry and Analysis of Banach Spaces.
p.
37.
Moltó, Aníbal
2019.
Descriptive Topology and Functional Analysis II.
Vol. 286,
Issue. ,
p.
225.
Gul'ko, Sergei P.
Ivanov, Aleksandr V.
Shulikina, Maria S.
and
Troyanski, Stanimir
2020.
Locally uniformly rotund renormings of the spaces of continuous functions on Fedorchuk compacts.
Topology and its Applications,
Vol. 281,
Issue. ,
p.
107211.