Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:27:04.299Z Has data issue: false hasContentIssue false
  • English
  • Français

On Isomorphisms of Abelian Group Algebras

Published online by Cambridge University Press:  20 November 2018

Eugene Spiegel
Eugene Spiegel*
Affiliation:
University of Connecticut, Storrs, Connecticut
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For F a field and G a group, let FG = F(G) be the group algebra of G over F. It 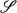is a class of finite abelian groups, F induces an equivalence relation on 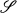by 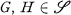are equivalent if and only if FG ⋍ FH. We will call two fields F and K equivalent on 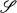if they induce the same equivalence relation on We will say F is equivalent to isomorphism on 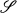if FG ⋍ FH if and only if G ⋍ H for any two elements .

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 1 , 01 February 1975 , pp. 155 - 161
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. May, W., Commutative group algebras, Trans. Amer. Math. Soc. 136 (1969), 139–149.Google Scholar
2. Perlis, S. and Walker, G., Abelian group algebras of finite order, Trans. Amer. Math. Soc. 68 (1950), 420–426.Google Scholar
3. Ribenboim, P., Algebraic numbers (Wiley-Interscience, New York, 1972).Google Scholar
4. Spiegel, E., Abelian p-adic group rings (to appear in Comment. Math. Helv.).Google Scholar