No CrossRef data available.
Article contents
On Hilbert Covariants
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 
$F$ denote a binary form of order 
$d$ over the complex numbers. If 
$r$ is a divisor of $d$, then the Hilbert covariant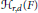 
${{H}_{r,\,d}}\,\left( F \right)$ vanishes exactly when $F$ is the perfect power of an order $r$ form. In geometric terms, the coefficients of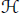 
$H$ give defining equations for the image variety 
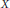$X$ of an embedding 
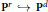${{\text{P}}^{r}}\,\to \,{{\text{P}}^{d}}$. In this paper we describe a new construction of the Hilbert covariant and simultaneously situate it into a wider class of covariants called the Göttingen covariants, all of which vanish on 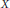$X$. We prove that the ideal generated by the coefficients of 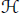$H$ defines 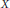$X$ as a scheme. Finally, we exhibit a generalisation of the Göttingen covariants to 
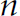$n$-ary forms using the classical Clebsch transfer principle.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
References
[1]
Abdesselam, A., On the volume conjecture for classical spin networks.
J. Knot Theory Ramifications
21, 1250022, 2012. http://dx.doi.org/10.1142/S0218216511009522
Google Scholar
[2]
A. Abdesselam, and Chipalkatti, J., Brill–Gordan loci, transvectants and an analogue of the Foulkes conjecture.
Adv. Math.
208(2007), 491–520. http://dx.doi.org/10.1016/j.aim.2006.03.003
Google Scholar
[3]
A. Abdesselam, , On the Wronskian combinants of binary forms.
J. Pure Appl. Algebra
210(2007), 43–61.
http://dx.doi.org/10.1016/j.jpaa.2006.08.006
Google Scholar
[4]
Aluffi, P. and Faber, C., Linear orbits of d-tuples of points in P1.
J. Reine Angew. Math.
445(1993), 205–220.Google Scholar
[5]
Arbarello, E., Cornalba, M., Griffiths, P.A., and Harris, J., Geometry of Algebraic Curves, Vol. I.
Grundlehren Math.Wiss.
267, Springer-Verlag, New York, 1985.Google Scholar
[6]
Briand, E., Covariants vanishing on totally decomposable forms.
In: Liaison, Schottky Problem and Invariant Theory, Progr. Math.
280, Birkh–user, Basel, 2010, 237–256.Google Scholar
[7]
Brioschi, F., Sopra un teorema del sig. Hilbert.
Rendiconti del Circolo Matematico di Palermo tomo
X(1896), 153–157.Google Scholar
[8]
Chipalkatti, J., On Hermite's invariant for binary quintics.
J. Algebra
317(2007), 324–353. http://dx.doi.org/10.1016/j.jalgebra.2007.06.021
Google Scholar
[9]
Chipalkatti, J., On the saturation sequence of the rational normal curve.
J. Pure Appl. Algebra
214(2010), 1598–1611. http://dx.doi.org/10.1016/j.jpaa.2009.12.005
Google Scholar
[10]
Clebsch, A., Ueber symbolische Darstellung algebraischer Formen.
J. Reine Angew. Math. vol.
59, pp. 1–62, 1861.Google Scholar
[11]
Dolgachev, I., Lectures on Invariant Theory.
London Math. Soc. Lecture Note Ser.
296, Cambridge University Press, 2003.Google Scholar
[12]
Dolgachev, I., Classical Algebraic Geometry: A Modern View.
Cambridge University Press, Cambridge, 2012.Google Scholar
[13]
Eisenbud, D., Commutative Algebra with a View Toward Algebraic Geometry.
Graduate Texts in Math.
150, Springer-Verlag, New York, 1995.Google Scholar
[14]
Eisenbud, D., The Geometry of Syzygies.
Graduate Texts in Math.
229, Springer-Verlag, New York, 2005.Google Scholar
[15]
Fisher, C. S., The death of a mathematical theory: A study in the sociology of knowledge.
Arch. Hist. Exact Sci.
3(1966), 137–159. http://dx.doi.org/10.1007/BF00357267
Google Scholar
[16]
Fulton, W. and Harris, J., Representation Theory, A First Course.
Graduate Texts in Math.
129
Springer-Verlag, New York, 1991.Google Scholar
[18]
Grace, J. H. and Young, A., The Algebra of Invariants.
Chelsea Publishing Co., New York, 1962.Google Scholar
[19]
Hilbert, D.,Ueber die notwendigen und hinreichenden covarianten Bedingungen für die Darstellbarkeit einer binären Form als vollständiger Potenz.
Math. Ann.
27(1886), 158–161. http://dx.doi.org/10.1007/BF01447309
Google Scholar
[20]
Hilbert, D., Theory of Algebraic Invariants.
Cambridge University Press, Cambridge, 1993.Google Scholar
[21]
Knapp, A., Lie Groups Beyond an Introduction.
Second edition.
Birkhäuser, Boston, 2002.Google Scholar
[22]
Kung, J. P. S. and Rota, G.-C., The invariant theory of binary forms.
Bull. Amer. Math. Soc. (N.S.)
10(1984), 27–85. http://dx.doi.org/10.1090/S0273-0979-1984-15188-7
Google Scholar
[23]
Littlewood, D. E., Invariant theory, tensors and group characters.
Philos. Trans. Roy. Soc. London Ser. A
239(1944), 305–365. ttp://dx.doi.org/10.1098/rsta.1944.0001
Google Scholar
[24]
MacDonald, I. G., Symmetric Functions and Hall polynomials.
Second edition. Oxford University Press, New York, 1995.Google Scholar
[25]
Meulien, M., Sur la complication des algèbres d‘invariants combinants.
J. Algebra
284(2005), 284–295. http://dx.doi.org/10.1016/j.jalgebra.2004.08.003
Google Scholar
[26]
Olver, P., Classical Invariant Theory.
London Math. Soc. Stud.
Texts, Cambridge University Press, Cambridge, 1999.Google Scholar
[27]
Processi, C., Lie Groups, an Approach Through Invariants and Representations.
Universitext, Springer-Verlag, New York, 2007.Google Scholar
[28]
Rota, G.-C., Two Turning Points in Invariant Theory.
Math. Intelligencer
21(1999), 20–27. http://dx.doi.org/10.1007/BF03024826
Google Scholar
[29]
Salmon, G., Exercises in the hyperdeterminant calculus.
Cambridge and Dublin Math. J.
9(1854), 19–33.Google Scholar
[30]
Salmon, G., Lessons Introductory to Higher Algebra.
Chelsea Publishing Co., New York, 1965.Google Scholar
[31]
B. Sturmfels, , Algorithms in Invariant Theory.
Texts Monogr. Symbol. Comput., Springer-Verlag, Wien–New York, 1993.Google Scholar
You have
Access