Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:51:04.608Z Has data issue: false hasContentIssue false
  • English
  • Français

On Group Rings

Published online by Cambridge University Press:  20 November 2018

D. B. Coleman
D. B. Coleman*
Affiliation:
University of Kentucky, Lexington, Kentucky
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a commutative ring with unity and let G be a group. The group ring RG is a free R-module having the elements of G as a basis, with multiplication induced by

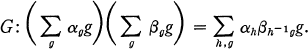
The first theorem in this paper deals with idempotents in RG and improves a result of Connell. In the second section we consider the Jacobson radical of RG, and we prove a theorem about a class of algebras that includes RG when G is locally finite and R is an algebraically closed field of characteristic zero. The last theorem shows that if R is a field and G is a finite nilpotent group, then RG determines RP for every Sylow subgroup P of G, regardless of the characteristic of R.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 2 , 01 April 1970 , pp. 249 - 254
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Amitsur, S. A., On the semi-simplicity of group algebras, Michigan Math. J. 6 (1959), 251–253.Google Scholar
2. Coleman, D. B., Finite groups with isomorphic group algebras, Trans. Amer. Math. Soc. 105 (1962), 1–8.Google Scholar
3. Connell, I. G., On the group ring, Can. J. Math. 15 (1963), 650–685.Google Scholar
4. Curtis, C. W. and Reiner, I., Representation theory of finite groups and associative algebras (Wiley (Interscience), New York, 1962).Google Scholar
5. Jacobson, N., Structure of rings, Amer. Math. Soc. Colloq. Publ., Vol. 37 (Amer. Math. Soc, Providence, R.I., 1964).Google Scholar
6. Passman, D. S., On the semi-simplicity of modular group algebras, Proc. Amer. Math. Soc. 20 (1969), 515–519.Google Scholar
7. Passman, D. S., On the semisimplicity of modular group algebras. II, Can. J. Math. 21 (1969), 1137—1145.Google Scholar
8. Perlis, P. and Walker, G. L., Abelian group algebras of finite order, Trans. Amer. Math. Soc. 68 (1950), 420–426.Google Scholar