Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:46:14.665Z Has data issue: false hasContentIssue false
  • English
  • Français

On Gaussian and Geodesic Curvature of Riemannian Manifolds

Published online by Cambridge University Press:  20 November 2018

Hansklaus Rummler
Hansklaus Rummler*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1], S. S. Chern gave a very elegant and simple proof of the Gauss-Bonnet formula for closed (i.e. compact without boundary) oriented Riemannian manifolds of even dimension:

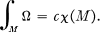
Here, c is a suitable constant depending on the dimension of M and Ω is an n-form (n = dim M) which may be calculated from its curvature tensor. W. Greub gave a coordinate-free description of this integrand Ω (cf. [4]).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 3 , June 1974 , pp. 629 - 635
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Chern, S. S., A simple intrinsic proof of the Gauss-Bonnet formula for closed Riemannian manifolds, Ann. of Math. 45 (1944), 747–752.Google Scholar
2. Chern, S. S., On the curvatura intégra in a Riemann manifold, Ann. of Math. 46 (1945), 674–684.Google Scholar
3. Chern, S. S., On curvature and characteristic classes of a Riemann manifold, Abh. Math. Sem. Univ. Hamburgh (1955), 117-126.Google Scholar
4. Greub, W. H., Zür Théorie der linear en Uebertragungen, Ann. Acad. Sci. Fenn. Ser. A. I. 846 (1964), 3–32.Google Scholar
5. Greub, W. H., Multilinear algebra (Springer, Berlin, Heidelberg, New York, 1967),Google Scholar
6. Hicks, N. J., Notes on differential geometry (Van Nostrand, New York, 1965).Google Scholar
7. Holmann, H. and Rummler, H., Differential﹜or men, Bibliographisches Institut, Mannheim, 1972.Google Scholar