Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T00:54:56.061Z Has data issue: false hasContentIssue false
  • English
  • Français

On Functional Cesàro And Hölder Methods of Summability

Published online by Cambridge University Press:  20 November 2018

D. Borwein  and
B. L. R. Shawyer
D. Borwein
Affiliation:
The University of Western Ontario, London, Ontario
B. L. R. Shawyer
Affiliation:
The University of Western Ontario, London, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that f(x) is integrable L in every finite interval [0, X], and that δ > 0. Define

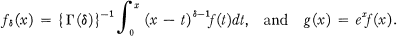
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 5 , 01 October 1976 , pp. 1058 - 1061
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Borwein, D., On methods of summability based on integral functions, II, Proc. Cambridge Philos. Soc. 56 (1960), 125–131.Google Scholar
2. Hardy, G. H., Divergent series (Oxford, 1949).Google Scholar
3. Riesz, M., Sur un théorème de la moyenne et ses applications, Acta Sci. Math. (Szeged) 1 (1923), 114–126.Google Scholar
4. Rogosinski, W. W., On Hausdorff's methods of summability, II, Proc. Cambridge Philos. Soc. 38 (1942), 344–363.Google Scholar
5. Shawyer, B. L. R., Iteration products of methods of summability and natural scales, Manuscripta Math. 13 (1974), 355–364.Google Scholar
6. Shawyer, B. L. R., On the product of the Cesar o and B or el-type methods of summability, J. London Math. Soc. (2) 7 (1973), 111–116.Google Scholar