Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Brauer, Richard
1964.
Some applications of the theory of blocks of characters of finite groups. II.
Journal of Algebra,
Vol. 1,
Issue. 4,
p.
307.
Brauer, Richard
1966.
Some applications of the theory of blocks of characters of finite groups III.
Journal of Algebra,
Vol. 3,
Issue. 2,
p.
225.
Brauer, Richard
1967.
�ber endliche lineare Gruppen von Primzahlgrad.
Mathematische Annalen,
Vol. 169,
Issue. 1,
p.
73.
Cline, E
and
Keller, G
1969.
A characterization of PSL(2, 8).
Journal of Algebra,
Vol. 13,
Issue. 3,
p.
393.
Leonard, Henry S
1972.
Finite linear groups having an abelian Sylow subgroup.
Journal of Algebra,
Vol. 20,
Issue. 1,
p.
57.
Lindsky, J.H
1972.
Complex linear groups of degree p + 1.
Journal of Algebra,
Vol. 20,
Issue. 1,
p.
24.
Leonard, Henry S
1973.
Finite linear groups having an abelian Sylow subgroup. II.
Journal of Algebra,
Vol. 26,
Issue. 2,
p.
368.
Feit, Walter
1974.
On finite linear groups II.
Journal of Algebra,
Vol. 30,
Issue. 1-3,
p.
496.
Sibley, David A
1974.
Certain finite linear groups of prime degree.
Journal of Algebra,
Vol. 32,
Issue. 2,
p.
286.
Sibley, David A
1975.
Finite linear groups with a strongly self-centralizing Sylow subgroup.
Journal of Algebra,
Vol. 36,
Issue. 1,
p.
158.
Sibley, David A
1975.
Finite linear groups with a strongly self-centralizing sylow subgroup. II.
Journal of Algebra,
Vol. 36,
Issue. 2,
p.
319.
LEONARD, HENRY S.
1976.
Proceedings of the Conference on Finite Groups.
p.
431.
Leon, Jeffrey S
1977.
Groups of order paqbr2.
Journal of Algebra,
Vol. 49,
Issue. 1,
p.
46.
Ferguson, Pamela A
and
Smith, Stephen D
1979.
Strongly self-centralizing Sylow 3-groups.
Journal of Algebra,
Vol. 58,
Issue. 2,
p.
572.
Ferguson, Pamela A
1980.
On finite complex linear groups of degree (q−1)2.
Journal of Algebra,
Vol. 63,
Issue. 2,
p.
287.
1992.
Group Representations Volume 1 Part B: Introduction to Group Representations and Characters.
Vol. 175,
Issue. ,
p.
1231.
Ivko, M. N.
and
Senashov, V. I.
1995.
On a new class of infinite groups.
Ukrainian Mathematical Journal,
Vol. 47,
Issue. 6,
p.
875.
Senashov, V. I.
1999.
Sufficient conditions for the almost layer finiteness of groups.
Ukrainian Mathematical Journal,
Vol. 51,
Issue. 4,
p.
525.
Сенашов, В. И.
1999.
Достаточные условия почти слойной конечности группы.
Ukrainian Mathematical Journal,
Vol. 51,
Issue. 4,
p.
472.
Сенашов, Владимир Иванович
and
Senashov, Vladimir Ivanovich
2002.
Строение бесконечной силовской подгруппы в некоторых периодических группах Шункова.
Дискретная математика,
Vol. 14,
Issue. 4,
p.
133.
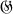 of order of g which satisfy the following condition:
of order of g which satisfy the following condition: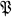 of
of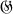 then the centralizer
then the centralizer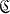 (P) of P in
(P) of P in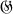 coincides with the centralizer
coincides with the centralizer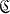 (
(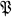 ) of
) of 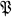 in
in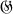 .
.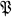 is abelian. It is possible to obtain rather detailed information about the irreducible characters of groups
is abelian. It is possible to obtain rather detailed information about the irreducible characters of groups 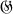 in this class (§ 4).
in this class (§ 4).

