Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cortadellas Benítez, Teresa
and
Zarzuela Armengou, Santiago
2007.
On the structure of the fiber cone of ideals with analytic spread one.
Journal of Algebra,
Vol. 317,
Issue. 2,
p.
759.
Zhu, Guangjun
2008.
On Fiber Coefficients of Fiber Cones†.
Communications in Algebra,
Vol. 36,
Issue. 11,
p.
4120.
Zhu, Guangjun
2008.
Depth of fiber cones of ideals with almost minimal mixed multiplicity.
Journal of Algebra,
Vol. 320,
Issue. 9,
p.
3534.
Viet, Duong Quoc
2009.
On the multiplicity and the Cohen–Macaulayness of fiber cones of graded algebras.
Journal of Pure and Applied Algebra,
Vol. 213,
Issue. 11,
p.
2104.
Zhu, Guangjun
2009.
Fiber Coefficients and Depth of Fiber Cones.
Communications in Algebra,
Vol. 37,
Issue. 10,
p.
3686.
Zhu, Guangjun
and
Tang, Zhongming
2010.
A Lower Bound on the Second Fiber Coefficient of the Fiber Cones.
Communications in Algebra,
Vol. 38,
Issue. 5,
p.
1919.
Trung, N.V.
and
Verma, J.K.
2010.
Hilbert functions of multigraded algebras, mixed multi- plicities of ideals and their applications.
Journal of Commutative Algebra,
Vol. 2,
Issue. 4,
VIET, Duong Quoc
and
THANH, Truong Thi Hong
2011.
MULTIPLICITY AND COHEN-MACAULAYNESS OF FIBER CONES OF GOOD FILTRATIONS.
Kyushu Journal of Mathematics,
Vol. 65,
Issue. 1,
p.
1.
Zhu, Guangjun
2011.
Primary Ideals with Good Fiber Cone.
Communications in Algebra,
Vol. 39,
Issue. 7,
p.
2276.
Cortadellas, Teresa
and
Zarzuela, Santiago
2011.
Apery and micro-invariants of a one-dimensional Cohen–Macaulay local ring and invariants of its tangent cone.
Journal of Algebra,
Vol. 328,
Issue. 1,
p.
94.
Jayanthan, A. V.
and
Nanduri, Ramakrishna
2012.
Castelnuovo–Mumford Regularity and Gorensteinness of Fiber Cone.
Communications in Algebra,
Vol. 40,
Issue. 4,
p.
1338.
Zhu, Guangjun
2013.
The Joint Reduction Number and Upper Bounds of Hilbert Series of Fiber Cones.
Algebra Colloquium,
Vol. 20,
Issue. 04,
p.
653.
Jayanthan, A. V.
and
Nanduri, Ramakrishna
2014.
On the depth of fiber cones of stretched m-primary ideals.
Indian Journal of Pure and Applied Mathematics,
Vol. 45,
Issue. 6,
p.
925.
Montaño, Jonathan
2015.
Artin–Nagata properties, minimal multiplicities, and depth of fiber cones.
Journal of Algebra,
Vol. 425,
Issue. ,
p.
423.
Balakrishnan, R.
and
Jayanthan, A. V.
2018.
On the Vasconcelos inequality for the fiber multiplicity of modules.
Communications in Algebra,
Vol. 46,
Issue. 8,
p.
3322.
D’Cruz, Clare
and
Guerrieri, Anna
2019.
Homology, mixed multiplies and Hilbert coefficients of the fiber cone.
Journal of Algebra and Its Applications,
Vol. 18,
Issue. 04,
p.
1950061.
Miranda-Neto, Cleto B.
2020.
On Special Fiber Rings of Modules.
Canadian Journal of Mathematics,
Vol. 72,
Issue. 1,
p.
225.
Abdolmaleki, Reza
and
Kumashiro, Shinya
2024.
Defining ideals of Cohen–Macaulay fiber cones.
International Journal of Algebra and Computation,
Vol. 34,
Issue. 07,
p.
1099.
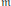 $\text{m}$-Primary Ideals
$\text{m}$-Primary Ideals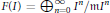 $F\left( I \right)\,=\,\oplus _{n=0}^{\infty }{{I}^{n}}/\text{m}{{I}^{n}}$ of an
$F\left( I \right)\,=\,\oplus _{n=0}^{\infty }{{I}^{n}}/\text{m}{{I}^{n}}$ of an 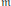 $\text{m}$-primary ideal of a
$\text{m}$-primary ideal of a  $d$-dimensional Cohen–Macaulay local ring
$d$-dimensional Cohen–Macaulay local ring 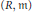 $\left( R,m \right)$ are derived in terms of the mixed multiplicity
$\left( R,m \right)$ are derived in terms of the mixed multiplicity 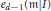 ${{e}_{d-1}}\left( \text{m }|I \right)$, the multiplicity
${{e}_{d-1}}\left( \text{m }|I \right)$, the multiplicity 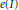 $e\left( I \right)$, and superficial elements. As a consequence, the Cohen–Macaulay property of
$e\left( I \right)$, and superficial elements. As a consequence, the Cohen–Macaulay property of 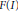 $F\left( I \right)$ when
$F\left( I \right)$ when  $I$ has minimal mixed multiplicity or almost minimal mixed multiplicity is characterized in terms of the reduction number of
$I$ has minimal mixed multiplicity or almost minimal mixed multiplicity is characterized in terms of the reduction number of  $I$ and lengths of certain ideals. We also characterize the Cohen–Macaulay and Gorenstein properties of fiber cones of
$I$ and lengths of certain ideals. We also characterize the Cohen–Macaulay and Gorenstein properties of fiber cones of 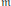 $\text{m}$-primary ideals with a
$\text{m}$-primary ideals with a  $d$-generated minimal reduction
$d$-generated minimal reduction 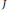 $J$ satisfying
$J$ satisfying 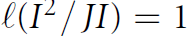 $\ell \left( {{I}^{2}}/JI \right)\,=\,1$ or
$\ell \left( {{I}^{2}}/JI \right)\,=\,1$ or 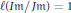 $l\left( Im \right)Jm) = 1$.
$l\left( Im \right)Jm) = 1$.